Матричное представление линейных кодов

В п. 2.5.1 образующая матрица (2.28) составлена путем простого подбора КВ в соответствии с предъявляемыми к ним требованиями. Такое решение задачи приемлемо при небольшом объеме кода, но становится мало пригодном при его существенном увеличении. Соответственно, возникнут трудности и при составлении контрольной матрицы H.

Для упрощения указанных операций групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода 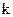и 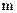. Число строк матрицы равно 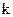, число столбцов равно .

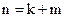Теорией и практикой установлено, что для упрощения процесса кодирования наиболее удобно, чтобы порождающая матрица 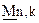состояла из двух матриц: единичной матрицы размерности 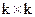и дописываемой справа матрицы-дополнения (контрольной подматрицы) размерности 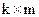, которая соответствует 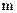проверочным разрядам:

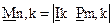(2.40)

Единичной матрицей 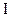называется квадратная матрица, у которой по одной из диагоналей расположены только единицы, а все остальные элементы равны нулю. Учитывая это, запишем порождающую матрицу 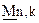в виде:

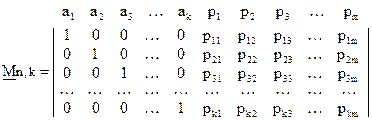(2.41)

Характерной особенностью данной матрицы является то, что в порождаемых ею разрешенных кодовых комбинациях первые 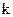символов совпадают с исходными информационными, а последующие 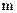символов оказываются проверочными. Это утверждение следует из того, что разрешенные КВ, соответствующие произвольной комбинации 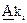из 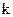информационных символов, получают путем умножения вектора 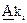на порождающую матрицу :

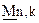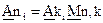. (2.42)

В общем случае, при перемножении матрицы 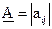размерности 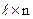и матрицы 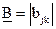размерности 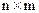, элементами 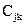матрицы-произведения размерности 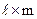являются суммы произведений элементов i-й строки матрицы 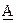на соответствующие элементы k-го столбца матрицы :

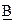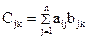. (2.43)

Пусть 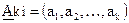. Умножив вектор-строку 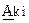на матрицу 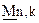, получим вектор 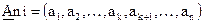, где проверочные символы 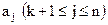являются линейными комбинациями информационных, определяемыми в соответствии с выражением:

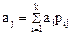. (2.44)

Таким образом, при использовании порождающей матрицы (2.41) формирование разрешенных КВ линейного кода сводится к добавлению к k-значной информационной комбинации m контрольных символов, определяемых в соответствии с выражением (2.44).

При составлении матрицы 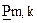необходимо учитывать, что для обеспечения требуемого кодового расстояния кода вес каждой строки матрицы 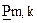должен быть не менее 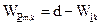, где d – требуемое кодовое расстояние кода; 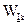– вес соответствующей строки матрицы 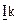(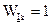). Если бы в матрице (2.41) левая половина была бы не единичной матрицей, а имела вес 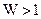, это усложнило бы как построение кода, так и техническую реализацию кодера и декодера.

Дополнительно следует иметь в виду, что чем больше вес строк матрицы 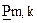, тем ближе порождаемый код к совершенному (плотноупакованному, оптимальному), обеспечивающему максимально возможную корректирующую способность при заданной избыточности. В связи с этим рекомендуется из всех возможных m-значных кодовых комбинаций в качестве строк матрицы 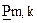выбирать комбинации, обладающие наибольшим весом. Это обеспечивает требуемое кодовое расстояние между КВ матрицы (2.41), а использование в (2.41) единичной матрицы 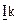гарантирует их линейную независимость.

Пример.

Построить порождающую матрицу линейного группового кода, исправляющего однократную ошибку (d = 3), если требуемый объем кода .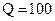

Решение.

Для передачи 100 сообщений необходимо соблюдать неравенство (2.23):

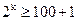, откуда .

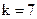В соответствии с (2.25) требуемое число контрольных разрядов:

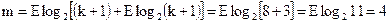
Таким образом, число строк порождающей матрицы 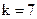, число столбцов .

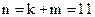Учитывая вышеизложенное, записываем порождающую матрицу 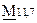в виде:

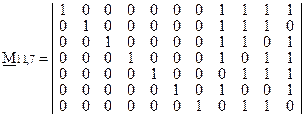(2.45)

По известной матрице 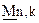контрольная матрица 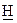определяется в соответствии с выражением:

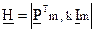, (2.46)

где 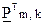– транспонированная матрица 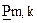(в транспонированной матрице строками являются столбцы, а столбцами – строки исходной матрицы); 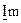– единичная матрица размерности .

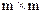Для порождающей матрицы (2.45) контрольная матрица 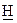имеет вид:

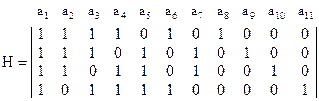(2.47)

В соответствии с (2.47) контрольные символы определяются выражениями:

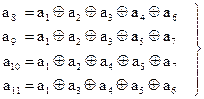(2.48)

Элементы синдрома вычисляются по уравнениям:

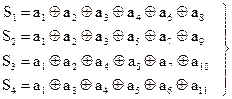(2.49)

Пример.

Закодировать число 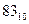линейным кодом, использующим контрольную матрицу (2.47).

Решение.

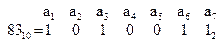
В соответствии с (2.48) получаем:

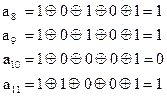
Кодовый вектор, отображающий заданное число:

.

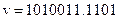Предположим, что при передаче найденного КВ произошло искажение 4-го разряда, т.е. принятый КВ имеет вид:

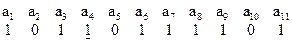
По (2.49) находим синдром:

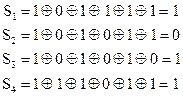
Найденный синдром 1011 совпадает с 4-м столбцом контрольной матрицы (2.47), следовательно, декодирование выполнено верно.

Построение контрольной матрицы для кодов с большей корректирующей способностью осуществляется аналогично.

Пример.

Построить контрольную матрицу линейного кода, исправляющего одиночные и двойные ошибки. Требуемое число информационных разрядов .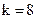

Решение.

Для построения порождающей матрицы необходимо определить число контрольных разрядов. При заданной корректирующей способности кода величина m определяется по (2.26), т.е. 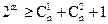. Расчеты показывают, что при 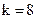минимальное значение m, при котором выполняется неравенство (2.26), равно 7. Следовательно, 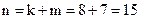. В соответствии с вышеизложенным, матрица 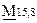имеет вид:

=

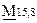(2.50)

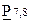При построении матрицы 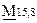учтено, что для получения требуемой корректирующей способности кодовое расстояние кода, согласно (2.21), 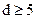. Следовательно, вес векторов подматрицы 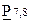должен быть не менее 4.

Контрольная матрица 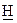имеет вид:

–

номера разрядов

=

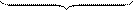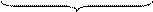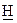(2.51)

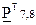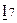В соответствии с (2.51) составляем выражения для контрольных разрядов.

Обозначим 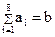. Тогда получаем:

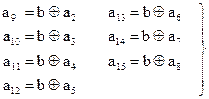(2.52)

Элементы синдрома вычисляются по уравнениям:

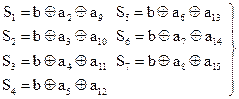(2.53)

При однократных ошибках синдром совпадает с соответствующим столбцом контрольной матрицы, а синдром двойной ошибки равен сумме по модулю 2 синдромов ошибочных разрядов. Очевидно, что при использовании матрицы (2.51) синдромы одиночных и двойных ошибок не совпадают, что позволяет однозначно исправлять как одиночные, так и двойные ошибки.

Рассмотрим примеры.

Пример 1.

Закодировать по (2.51) безизбыточный КВ

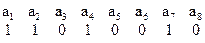
Решение.

Определяем .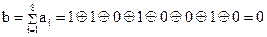

Определяем по (2.52) контрольные разряды:

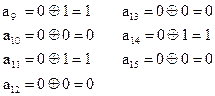
Полный КВ имеет вид:

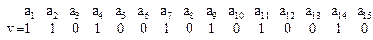
Пример 2.

При передаче вектора 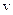произошло искажение 5-го разряда, т.е. принятый КВ имеет вид:

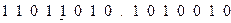
Выполнить декодирование.

Решение.

Определяем по принятому КВ 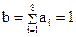. Определяем по (2.53) синдром:

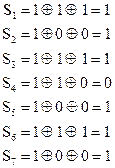
Найденный синдром совпадает с 5-м столбцом матрицы (2.51), что подтверждает правильность декодирования.

Пример 3.

При передаче КВ произошло искажение 5-го и 7-го разрядов, т.е. принятый КВ имеет вид:

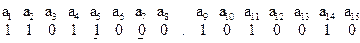
Выполнить декодирование.

Решение.

По принятому КВ определяем 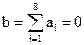. Определяем синдром:

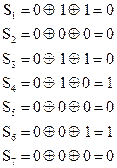
Полученный синдром не нулевой, следовательно, есть ошибка. В контрольной матрице (2.51) таких столбцов нет, значит произошла двойная ошибка.

Проверка:

								–	синдром ошибки 5-го разряда
							–	синдром ошибки 7-го разряда
								–	синдром ошибки 5-го и 7-го разрядов

Вывод – декодирование выполнено верно.

При практической реализации синдромного метода декодирования все возможные синдромы ошибок нужно заранее рассчитать и хранить в каком-нибудь запоминающем устройстве, например, в ПЗУ. В последнем случае на адресные входы ПЗУ нужно подавать синдром, а матрица ПЗУ должна быть закодирована так, чтобы 1 появлялись только на выходах, соответствующих ошибочным разрядам (при этом совмещаются функции ЗУ и ДШ).

Исправление ошибок осуществляется с помощью сумматоров по модулю 2 (см. п. 2.5.4).