Основные понятия и определения. Классификация кодов и их основные параметры

Квантованный АИМ-2 сигнал, в принципе, можно считать кодовым с основанием кода, равным числу М разрешенных уровней (уровней кван­тования) и с числом символов в кодовой группе, равным единице. Таким образом, квантованный сигнал является многоуровневым.

Многоуровневые сигналы весьма неудобны для передачи, так как при­емник должен различать все разрешенные уровни. Кроме того, такие сиг­налы трудно восстановить (регенерировать), если они подверглись воз­действию помех. Иными словами, многоуровневым сигналам в большой степени свойственны недостатки аналоговых сигналов. Поэтому в ЦСП обычно используются коды со сравнительно малым основанием, чаще всего двоичные. Процесс преобразования многоуровневого сигнала в код с низким основанием называется кодированием. Результатом кодирования является комбинация символов (посылок, цифр), представляющая в соот­ветствующей системе счисления номер разрешенного уровня квантован­ного сигнала. В ЦСП с ИКМ-ВРК широкое применение нашла двоичная система счисления. Запись любого квантованного уровня с М разрешен­ными уровнями в двоичной системе счисления может быть представлена в виде

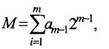(1.63)

где т - число разрядов кода; а,- - разрядная цифра, принимающая значе­ние 0 или 1. С помощью /и-разрядного двоичного кода можно закодиро­вать число уровней квантования, равное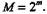

Поскольку выбор числа уровней квантования определяется допусти­мой величиной шага квантования, обычно приходится решать обратную задачу: определение минимально необходимого числа разрядов кода, ко­торый может быть использован для кодирования при заданном М. Оче­видно, что для двоичного кода имеем

(1-64)

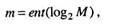
здесь ent означает большее целое число от выражения в круглых скобках.

Общее число кодовых групп или кодовых комбинаций равно М = 2^т.

Пример. Требуется определить необходимое число разрядов дво­ичного кода для кодирования числа 111 и записать его двоичным кодом.

Решение. Необходимое число разрядов согласно (9.64) будет рав­но: 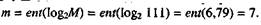Запись числа 111 соглас­но (1.63) будет иметь вид

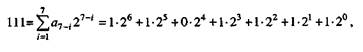
т.е. ему соответствует кодовая комбинация 1101111 со следующими наче-ниями разрядных цифр: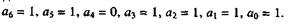

Набор величинможно рассматривать как ряд эталонных сигна-

лов с определенным 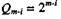номером разряда. Для нашего примера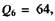

Однозначная связь величи­ныэталонного сигнала с номером разряда двоичного эквивалента раз­решенного квантованного уровня позволяет ограничиться передачей только ряда величин а„ составляющих кодовую комбинацию (или кодо­вую группу).

Множество используемых кодовых комбинаций, связанных единым законом построения, называется кодом. Простейшим кодом является код, в основе построения которого лежит отношение (1.63) и называется на­туральным двоичным кодом.

Графически коды удобно изображать кодовыми таблицами или ко­довыми растрами, характеризующими связь уровней квантования и соответствующих им кодовых комбинаций, представляя их по порядку уровней. Кодовые таблицы наиболее широко применяемых в ЦСП ко­дов приведены на рис. 1.23

Рис. 1.23. Таблицы двоичных кодов: а - натурального; б - кода Грея; в - симметричного

На рис. 1.23,а показана кодовая таблица 4-разрядного натурального двоичного кода, при помощи которого можно осуществить передачу 16 уровней. Здесь затемненные участки кодовой таблицы представляют 1 (единицы или импульсы), а незатемненные - 0 (нули или пробелы). Нуме­рация уровней дана сверху вниз, вверху указан вес разрядов кода.

Перестановка порядка следования кодовых комбинаций на обратный дает простой обратный код, веса разрядов которого показаны внизу. На­пример, уровень М = 11 в натуральном коде представляется кодовой ком­бинацией вида 1011 (см. рис. 1.23,а), обратный код будет иметь вид 1101.

Замена всех импульсов в кодовой комбинации на пробелы (или единиц на нули, а нулей на единицы) приводит к инверсному коду. Так, например, для М = 11 кодовая комбинация в инверсном коде имеет вид 0100. Другим типом кода, применяемого в ЦСП, является код Грея (он же рефлексный или зеркальный). Его отличительной особенностью является то, что лю­бые две соседние кодовые комбинации отличаются друг от друга лишь в одном разряде (рис. 1.23,6). Код Грея находит применение при кодирова­нии групповых телефонных и широкополосных телевизионных сигналов, для которых различие символов в большом числе разрядов кодовых групп соседних уровней квантования нежелательно, так как в этих случаях ошибки кодирования и декодирования особенно опасны. Но код Грея не

так легко декодировать. Поэтому его обычно преобразуют в натуральный двоичный код, декодирование которого особых трудностей не представ­ляет. Правило формирования кода Грея следующее: первые разряды оп­ределяют точно 2' блоков смежных уровней, разделенных посредством 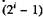порогов, а i-й разряд обозначает переход от единицы к нулю или наоборот на всех порогах, которые еще не определены переходами пре­дыдущих разрядов.

Преобразование кода Грея в натуральный двоичный код осуществля­ется следующим образом.

Если обозначить разряды двоичного натурального кода через а\...а_п, а разряды кода Грея через 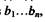то

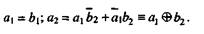
Символ Ф в правой части последнего выражения означает сложение по модулю 2, а эта операция тождественна логической функции исключи­тельное ИЛИ, представленной в средней части последнего выражения, аналогичное правило распространяется на все последующие разряды, а именно:

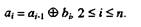
Сравнение таблиц натурального двоичного кода и кода Грея подсказы­вает довольно простое правило преобразования кода Грея в натуральный: в i-м разряде натурального кода формируется импульс или пробел в зави­симости от того, нечетным или четным было число импульсов в преды­дущих импульсных позициях комбинации кода Грея (включая i-ю пози­цию). Например, комбинации 1011001 кода Грея соответствует согласно этому правилу комбинация 1101110 натурального кода. Операция опреде­ления четности или нечетности числа импульсов может быть выполнена при помощи триггера.

Широкое применение при кодировании отсчетов нашли симметрич­ные коды (рис. 1.23,в). При кодировании двухполярных квантованных отсчетов оказывается удобным использовать высший разряд натурального двоичного кода для обозначения полярности отсчета, например использо­вать 1 для кодирования положительного отсчета и 0 - для отрицательного отсчета, а остальные разряды для кодирования абсолютной величины. Кодовая таблица симметричного кода оказывается симметричной относи­тельно своей середины. Из рис. 1.23,6 ясно, что код Грея обладает свойст­вом симметрии.

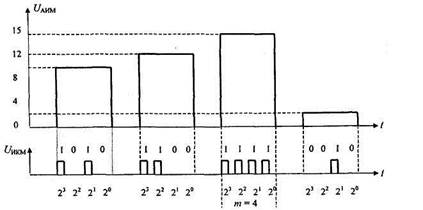
Рис. 1.24. Процесс кодирования отсчетов t/дим ^в кодовые комбинации {/тем

На рис. 1.24 приведены временные диаграммы, поясняющие процесс кодирования квантованного группового АИМ сигнала при использовании четырехразрядного натурального двоичного кода.

. Амплитуды отсчетов, поступающие на вход кодирующего устройства (кодера), принимают значения в диапазоне £/дим = 0...15 условных шагов квантования, а на выходе кодера формируется цифровой сигнал £/икм. представляющий последовательность четырехразрядных кодовых комби­наций. Последовательность /и-разрядных кодовых комбинаций на выходе кодера представляет собой групповой сигнал с импульсно-кодовой моду­ляцией, называемый цифровым.

Основными характеристиками кодов являются:

- кодовое расстояние, под которым понимается число разрядов, в ко­
торых различаются кодовые комбинации между собой; например, рас­
стояния между следующими друг за другом уровнями натурального дво­
ичного кода (рис. 1.23,а), равны 1, 2, 1, 3, 1, 2, 1, 4... и так далее. Наи­
большее расстоянием между соседними уровнями в от-разрядном нату­
ральном коде равно т и имеет место в середине кодовой таблицы. В коде
с единичным расстянием различие между двумя соседними кодовыми
комбинациями равно единице и имеет место только в одном разряде. Та­
ким является код Грея;

- избыточность кода, под которой понимается отношение максимально
возможного числа кодовых комбинаций при данной разрядности кода к
числу фактически используемых комбинаций. Код, в котором используется
весь ансамбль комбинаций (рис. 1.23), является неизбыточным;

- диспаритетность кодовой комбинации, т.е. превышение числа еди­
ниц над числом нулей; так, комбинации 000110 и 100111 имеют диспари-
терность - 2 и + 2, соответственно. Чем ниже диспаритетность, т.е. когда
число единиц и нулей приблизительно равно, тем легче решить проблемы
синхронизации по самим информационным сигналам;

- возможность обнаружения ошибок, т.е. по изменению структуры
кодовой комбинации можно судить о наличии ошибок. Для кода с посто­
янной диспаритетностью при искажении одного из разрядов кодовой ком­
бинации происходит изменение диспаритетности, что приводит к появле­
нию на приеме кодовой комбинации, не входящей в ансамбль используе­
мых кодовых комбинаций, что говорит о наличии ошибки. Если в 7-
разрядной кодовой комбинации имеется 4 единицы и 3 нуля, то любая
одиночная ошибка приводит к нечетному числу единиц. Поэтому, чтобы
убедиться, произошла или нет подобная ошибка, необходимо определить
нечетное или четное число принятых единиц. Этот метод носит название
проверки на четность;

- возможность исправления ошибок, т.е. по изменению структуры ко­
довой комбинации и кодового расстояния между соответствующими кодо­
выми комбинациями не только обнаруживается ошибка, но и устраняется.

Кодирование может быть линейным и нелинейным. Линейным кодиро­ванием называется кодирование равномерно квантованного сигнала, а нели­нейным - неравномерно квантованного сигнала. Кодирование может осуще­ствляться как на уровне индивидуального квантованного АИМ сигнала, так и на уровне группового квантованного АИМ сигнала. В первом случае ко­дек является индивидуальным, а во втором - групповым. Но и в том и дру­гом способах кодирования обязательно формируется групповой ИКМ сиг­нал, определенный на периоде дискретизации Г_д, называемым циклом.