Декодирование циклических кодов

Декодирование циклических кодов проводится путем деления принятого КВ на образующий многочлен. Если ошибки нет, то деление выполняется без остатка. Появление остатка сигнализирует об ошибке, исправление которой осуществляется в следующей последовательности.

Подсчитывается вес остатка 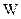. Если он равен или меньше кратности исправляемых ошибок, т.е. 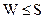, то принятый КВ складывают по модулю 2 с остатком и получают исправленный КВ.

Если 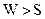, то производится циклический сдвиг на один символ влево и полученный после такого сдвига КВ снова делится на образующий многочлен. Если вес полученного остатка 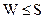, то циклически сдвинутую комбинацию складывают с остатком и полученный КВ циклически сдвигают в обратную сторону. В результате на исходной позиции получают исправленный КВ.

Если после первого сдвига и последующего деления на 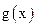вновь оказывается 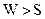, делается еще один сдвиг влево, снова проверяют остаток и так до тех пор, пока не окажется 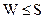. После сложения сдвинутой комбинации с остатком осуществляется ее сдвиг в обратную сторону на столько шагов, на сколько их было сделано до получения требуемого остатка.

Пример.

Предположим, что при передаче рассмотренного выше КВ 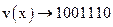произошло искажение 2-го разряда, т.е. принятый КВ 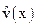имеет вид: 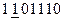. Определим истинный вид поступившего КВ.

Решение.

Согласно правилу, необходимо делить поступивший КВ на образующий многочлен и оценивать вес остатка. Выполняем:

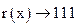. Остаток не нулевой, следовательно, есть ошибка.

Вес 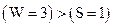– нужно осуществить циклический сдвиг принятой кодовой комбинации влево и повторить деление:

1)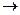

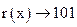. Опять 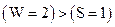, поэтому выполняем еще один циклический сдвиг влево и повторяем деление:

2)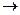

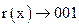. Здесь 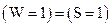, поэтому складываем сдвинутую кодовую комбинацию с остатком по модулю 2:

Полученную после суммирования комбинацию циклически сдвигаем вправо на 2 такта:

							– 1-ый сдвиг вправо
							– 2-ой сдвиг вправо

Исправленная кодовая комбинация – 1001110.

2.6.4. Циклические коды с .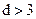

Циклические коды с d = 4. Эти коды могут обнаруживать одиночные, двойные и тройные ошибки или, в случае применения мажоритарного декодирования, обнаруживать двойные и исправлять одиночные ошибки.

Степень образующего многочлена и, соответственно, число контрольных разрядов в этом коде должно быть на единицу больше, чем для кода с :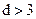

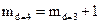. (2.60)

Образующий многочлен 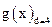равен произведению двучлена 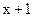на многочлен :

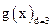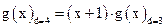(2.61)

Это объясняется тем, что двучлен 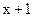позволяет обнаружить все одиночные и тройные ошибки, а многочлен 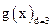– двойные ошибки. Так, для кода (7,3), обнаруживающего все тройные ошибки, можно выбрать .

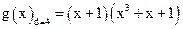Дальнейшая процедура кодирования остается такой же, как и в кодах с .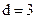

Пример.

Требуется закодировать сообщение 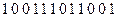циклическим кодом с .

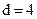Решение.

Определяем степень образующего многочлена для 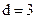по (2.25):

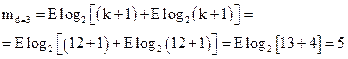
Выбираем из таблицы 2.4 образующий многочлен 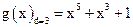. Тогда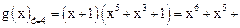
, .

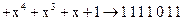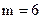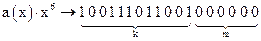
Разделив 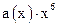на 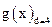, находим остаток:

.

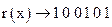Закодированная комбинация имеет вид:

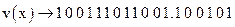, код (18,12).

Обнаружение ошибок производится по остаткам от деления принятой комбинации 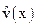на образующий многочлен 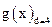. Если остаток нулевой, то контрольные разряды отбрасываются, а информационная часть используется по назначению. Если в результате деления получается ненулевой остаток, то комбинация бракуется.

Пример.

Пусть в рассмотренной выше комбинации кода (18,12) при передаче исказились 5, 7 и 11 разряды. Произведем декодирование.

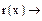Остаток ненулевой, поэтому комбинация бракуется.

Процесс исправления однократной ошибки и одновременного обнаружения двойной будет рассмотрен в п. 2.6.6 на примере кода (7,3).

Циклические коды с d 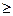5 позволяют обнаруживать и исправлять любое число ошибок. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем – разработчиков методики построения этих кодов). Построение кодов БЧХ отличается от построения циклических кодов с 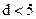только выбором образующего многочлена. Заданными при кодировании здесь являются кратность исправляемой ошибки 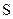и длина кодового слова n (на величину n при этом накладывается ряд ограничений). Числа информационных символов k и контрольных символов m подлежат определению.

Методика построения кодов БЧХ рассмотрена, например, в работах [6] и [8]. Декодирование кодов БЧХ производится по той же методике, что и декодирование циклических кодов с .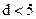

Коды БЧХ, предназначенные для исправления взаимно независимых ошибок, могут использоваться также для обнаружения и исправления пакетов ошибок. Однако более эффективными при решении этих задач являются специализированные коды, например, коды Файра [6] и коды Рида-Соломона [1]. При исправлении пакетов ошибок эти коды имеют значительно меньшую избыточность, чем коды БЧХ.