2015-01-21
485
В п. 2.3.2 образующая матрица (2.13) составлена путем простого подбора КВ в соответствии с предъявляемыми к ним требованиями. Такое решение задачи приемлемо при небольшом объеме кода, но становится малопригодным при его существенном увеличении. Соответственно, возникнут трудности и при составлении контрольной матрицы H.
Для упрощения указанных операций групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода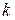 
и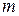 
. Число строк матрицы равно 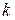, число столбцов равно 
.
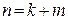Теорией и практикой установлено, что для упрощения процесса кодирования наиболее удобно, чтобы порождающая матрица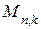 
состояла из двух матриц: единичной матрицы размерности 
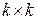и дописываемой справа матрицы-дополнения (контрольной подматрицы) размерности 
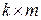, которая соответствует 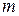проверочным разрядам:
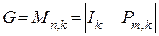(2.22)
Единичной матрицей I называется квадратная матрица, у которой по одной из диагоналей расположены только единицы, а все остальные элементы равны нулю.
При составлении матрицы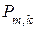 
рекомендуется из всех возможных m -значных кодовых комбинаций в качестве строк матрицы 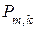выбирать комбинации, обладающие наибольшим весом. Это обеспечивает требуемое кодовое расстояние между КВ матрицы 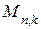, а использование в 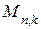единичной матрицы 
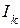гарантирует их линейную независимость.
По известной матрице 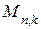контрольная матрица Н определяется в соответствии с выражением:
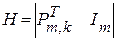, (2.23)
где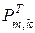 
– транспонированная матрица 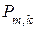(в транспонированной матрице строками являются столбцы, а столбцами – строки исходной матрицы );
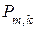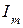– единичная матрица размером 
.
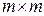Пример. Построить контрольную матрицу Н для линейного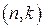 
-кода, исправляющего все одиночные ошибки, если требуемый объем кода Q=25.
Решение:
1. Определяем требуемое число информационных разрядов
, 
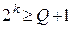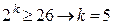
2. Определяем требуемое число контрольных разрядов m в соответствии с (2.11):
.
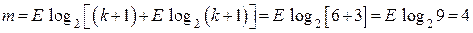Следовательно,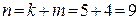 
. Код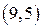 
.
Строим матрицу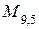 
в соответствии с (2.22):
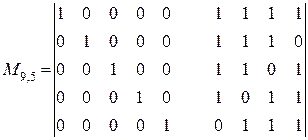(2.24)
По известной матрице 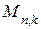строим контрольную матрицу в соответствии с (2.23):
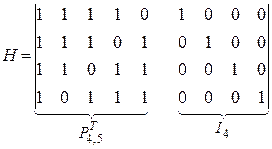(2.25)
