Формирование разрешенных кодовых комбинаций

Наиболее просто комбинации циклического кода можно получить, умножая многочлены 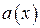, соответствующие комбинациям безизбыточного кода, на образующий многочлен . Такой способ легко реализуется, но код при этом получается неразделимым. Применительно к циклическим кодам принято отводить под информационные символы k старших разрядов, а под проверочные 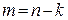младших разрядов. Чтобы получить такой разделимый код, применяется следующая процедура кодирования.

Многочлен 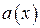, соответствующий k -разрядной комбинации безизбыточного кода, умножается на 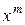, где 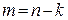. Затем произведение 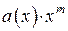делится на образующий многочлен . В общем случае при этом получается некоторое частное 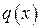и остаток 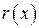. Последний складывается по модулю 2 с 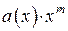и в результате получается многочлен

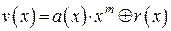. (2.30)

Полученный таким образом многочлен 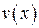делится на образующий многочлен без остатка. Действительно, многочлен 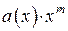можно записать в виде:

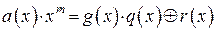(2.31)

Так как операции сложения и вычитания по модулю 2 тождественны, то 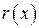из правой части равенства (2.31) можно перенести в левую. Тогда,

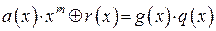, что и доказывает делимость 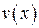на без остатка.

В комбинации 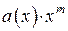m младших разрядов – нулевые, следовательно, разрешенные КВ циклического кода можно строить путем приписывания к комбинации безизбыточного кода 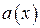остатка от деления многочлена 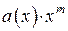на образующий многочлен кода.

Пример

Закодировать циклическим кодом, исправляющим однократную ошибку, комбинацию 1001.

Решение

Согласно заданию: 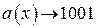, , 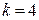требуемое кодовое расстояние кода .

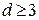Для того чтобы код был способен исправлять однократную ошибку, степень образующего многочлена m должна удовлетворять условию:

.

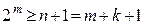Получаем: , .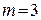

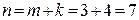Из табл. 2.4 выбираем неприводимый многочлен степени 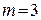и числом ненулевых членов, равным 3 ():

.

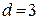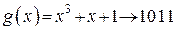Определим число различных остатков:

№ остатка

……

1 0 1 1

В дальнейшем остатки повторяются.

Количество различных остатков равно 7, следовательно, выбранный образующий многочлен входит в разложение многочлена 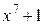и не входит в разложени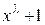е , где 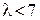, что и требуется.

Согласно (2.30), для определения комбинации циклического кода, соответствующей безизбыточной комбинации 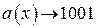, необходимо найти остаток 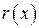от деления 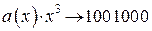на образующий многочлен 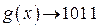и сложить его по модулю 2 с 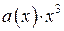. Имеем:

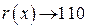, а искомая комбинация циклического кода – 1001110.

Разрешенные кодовые комбинации должны делиться на образующий многочлен без остатка. Проверим:

Вывод: кодирование выполнено правильно.