2015-01-21
566
Порядок статистической обработки результатов косвенных измерений можно представить следующим образом:
1. Статистическая обработка результатов прямых измерений и нахождение X ср i и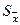 
i.
2. Расчет искомого значения ФВ (точечной оценки результата косвенных измерений)
Q = f (X ср1, X ср2, ..., X ср n).
3. Определение оценки каждой частной погрешности с учетом ее весового коэффициента
EXi =k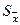i i,
где ki = дf/дXi
4. Определение оценки погрешности (среднего квадратического отклонения) результата косвенного измерения. Оценку погрешности результата косвенного измерения рассчитывают с учетом весовых коэффициентов частных погрешностей. При значимой стохастической связи оценка среднего квадратического отклонения (оценка погрешности косвенного измерения) рассчитывается с учетом коэффициента корреляции Rij (определяют традиционными статистическими расчетами)
.
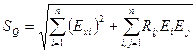При практическом отсутствии корреляции между величинами, получаемыми в результате прямых измерений
.
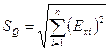5. Определение значения коэффициента Стьюдента t в зависимости от выбранной доверительной вероятности Р и запись результата косвенного измерения в установленной форме
Q = Q ср + t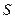 
Qi, Р = 0, ...
Результаты прямых и косвенных измерений должны отвечать требованиям обеспечения единства измерений, то есть в описании результата следует использовать узаконенные единицы физических величин и указывать оценки погрешностей. Информацию о единицах физических величин можно найти в нормативной документации, специальной и справочной литературе.
Стандартное определение единства измерений требует, чтобы погрешности были известны с заданной вероятностью, из чего следует:
· в описание результата входят только стохастически представляемые погрешности, значит, систематические составляющие по возможности должны быть исключены;
· неисключенные остатки систематической составляющей погрешности измерения могут входить в описание результата измерений как рандомизированные величины, значения которых соизмеримы со случайной составляющей погрешности измерения;
· если неисключенные остатки систематической составляющей погрешности измерения существенно меньше случайной составляющей, ими пренебрегают, но возможна (хотя и нежелательна) обратная ситуация, когда собственно случайная составляющая оказывается пренебрежимо малой по сравнению с неисключенной систематической составляющей.
