Показательными принято называть уравнения, в которых неизвестное входит только в показатели степеней при постоянных основаниях. Простейшим показательным уравнением является уравнение вида
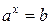 . (1)
. (1)
Его решением при 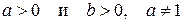 , является
, является 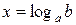 .
.
Некоторые показательные уравнения приводятся к виду (1) с помощью равенств:
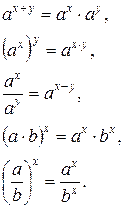
Многие показательные уравнения решаются методом приведения обеих частей к одному основанию.
Пример 1. Решить уравнение 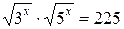 .
.
Решение. Поскольку 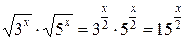 , то
, то
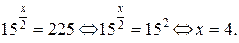
Ответ: 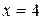 .
.
При решении простейших показательных уравнений используется преобразование, состоящее в вынесении общего множителя за скобки.
Пример 2. Решить уравнение 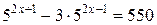 .
.
Решение. Вынося в левой части уравнения выражение 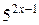 за скобки, получаем
за скобки, получаем
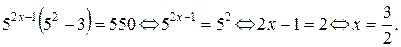
Ответ: 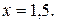
Уравнение вида
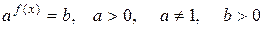 (2)
(2)
может быть решено при помощи логарифмирования обеих частей (это возможно, так как обе части уравнения положительны).
Логарифмируя, получаем уравнение 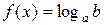 , равносильное уравнению (2).
, равносильное уравнению (2).
Пример 3. Решить уравнение 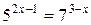 .
.
Решение. Обе части положительны, поэтому можно прологарифмировать его по основанию 5. Получим уравнение
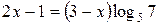 ,
,
равносильное исходному. Таким образом,
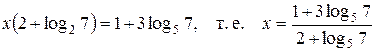 .
.
Ответ: 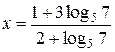 .
.
Если показательное уравнение имеет вид
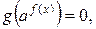 (3)
(3)
то его решение заменой 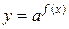 сводится к решению уравнения вида
сводится к решению уравнения вида
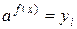 ,
,
где 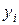 – корни уравнения
– корни уравнения 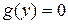 .
.
Пример 4. Решить уравнение 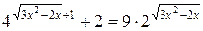 .
.
Решение. Обозначая 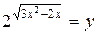 , получаем квадратное уравнение
, получаем квадратное уравнение
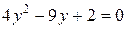 ,
,
корнями которого будут 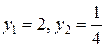 .
.
Таким образом, решение данного уравнения свелось к решению уравнений 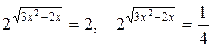 .
.
Второе уравнение решений не имеет, так как 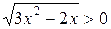 при всех допустимых значениях
при всех допустимых значениях 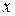 . Из одного уравнения следует другое
. Из одного уравнения следует другое
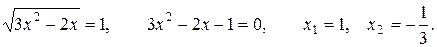
Проверкой убеждаемся, что эти корни удовлетворяют исходному уравнению.
Ответ: 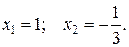
Показательные уравнения, основания степеней которых являются последовательными членами геометрической прогрессии, а показатели степеней одинаковы, делением на любой из крайних членов приводятся к уравнениям вида (3).
Пример 5. Решить уравнение 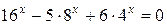 .
.
Решение. Разделим обе части уравнения на 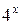 . Имеем
. Имеем
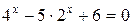 .
.
Обозначая 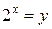 , получаем уравнение
, получаем уравнение 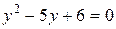 , корнями которого будут
, корнями которого будут 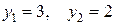 .
.
Таким образом, решение уравнения сводится к решению двух простейших показательных уравнений 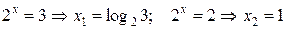 .
.
Ответ: 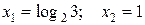 .
.
Пример 6. Решить уравнение 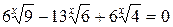 .
.
Решение.Область допустимых значений данного уравнения состоит из всех натуральных чисел, больших 1.
Разделив обе части уравнения на 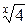 и положив
и положив 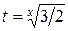 , получим уравнение
, получим уравнение 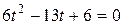 , корни которого
, корни которого 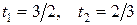 .
.
Таким образом, решение уравнения сводится к решению двух уравнений 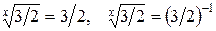 , которые решений не имеют.
, которые решений не имеют.
Ответ: нет решений.
Уравнения вида
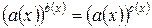 (4)
(4)
с множеством допустимых значений, определяемых условием 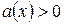 , логарифмированием обеих частей приводятся к эквивалентному уравнению
, логарифмированием обеих частей приводятся к эквивалентному уравнению
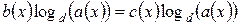 . (5)
. (5)
Последнее уравнение эквивалентно двум уравнениям:
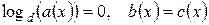 . (6)
. (6)
Пример 7. Решить уравнение 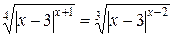 .
.
Решение. Множество допустимых значений неизвестного данного уравнения 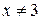 . Логарифмируя обе части уравнения по основанию 3 и приводя подобные члены, получаем
. Логарифмируя обе части уравнения по основанию 3 и приводя подобные члены, получаем 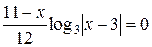 , которое эквивалентно двум уравнениям:
, которое эквивалентно двум уравнениям:
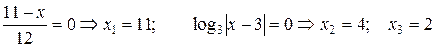 .
.
Ответ: 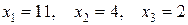 .
.
 2015-01-21
2015-01-21 4656
4656
