Логарифмическим уравнением называется уравнение, содержащее неизвестную величину под знаком логарифма. Простейшее логарифмическое уравнение
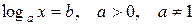 , (1)
, (1)
с множеством допустимых значений 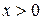 имеет решение
имеет решение 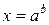 .
.
Логарифмическое уравнение, в котором под знаком логарифма стоит функция 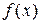 ,
,
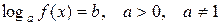 (2)
(2)
имеет множество допустимых значений 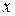 , задаваемых неравенством
, задаваемых неравенством 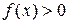 , и эквивалентно уравнению
, и эквивалентно уравнению 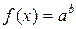 .
.
К простейшим логарифмическим уравнениям относятся также уравнения вида
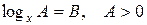 , (3)
, (3)
которые
а) при 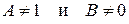 имеют единственный корень
имеют единственный корень 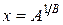 ;
;
б) при 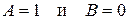 имеют решением любое положительное, отличное от единицы, число;
имеют решением любое положительное, отличное от единицы, число;
в) при 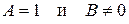 корней не имеют;
корней не имеют;
г) при 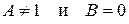 корней не имеют.
корней не имеют.
Пример 1. Решить уравнение 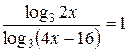 .
.
Решение. О.Д.З. исходного уравнения определяется системой
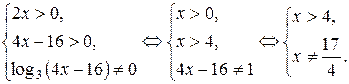
Перенесем все члены уравнения в левую часть и приведем их к общему знаменателю. Поэтому исходное уравнение равносильно системе
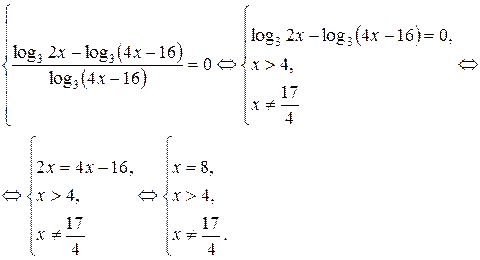
Число 8 – единственный корень исходного уравнения.
Ответ: 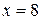 .
.
Если логарифмическое уравнение имеет вид
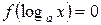 , (4)
, (4)
где 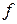 – некоторая функция, то заменой
– некоторая функция, то заменой 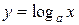 оно сводится к уравнениям вида (2)
оно сводится к уравнениям вида (2)
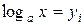 ,
,
где 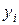 – корни уравнения
– корни уравнения 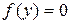 .
.
Аналогично решается уравнение вида
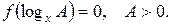 (5)
(5)
Пример 2. Решить уравнение 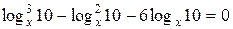 .
.
Решение. Обозначим 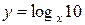 и произведем замену неизвестного в уравнении. Тогда
и произведем замену неизвестного в уравнении. Тогда
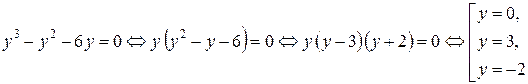 .
.
Возвращаясь к прежней переменной, имеем
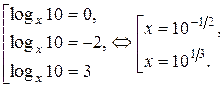
Ответ: 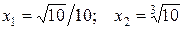 .
.
Логарифмическое уравнение вида
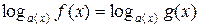 (6)
(6)
эквивалентно уравнению
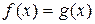 ,
,
рассматриваемому на множестве допустимых значений 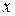 , задаваемом системой неравенств
, задаваемом системой неравенств
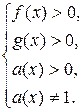
Если в данное уравнение входят логарифмы по разным основаниям, то предварительно необходимо привести все логарифмы к одному основанию.
Пример 3. Решить уравнение
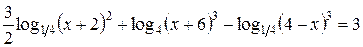 .
.
Решение. О.Д.З. уравнения определяется системой, решение которой следующее: 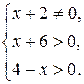
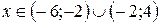 .
.
Переходя в уравнении к основанию 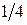 и используя формулу получаем
и используя формулу получаем
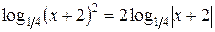 ,
,
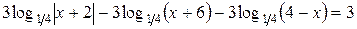 .
.
Последнее уравнение на О.Д.З. исходного уравнения равносильно системе
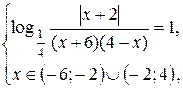
т. е. системе
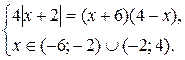
Таким образом, исходное уравнение равносильно совокупности двух систем:
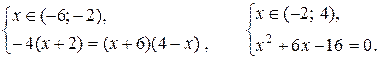
Первая система имеет решение 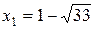 , вторая –
, вторая – 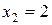 .
.
Ответ: 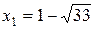 ,
, 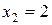 .
.
 2015-01-21
2015-01-21 692
692








