Задание 1. Сечения составных балок из стальных профилей

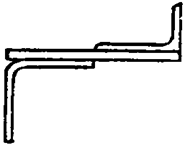
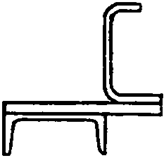
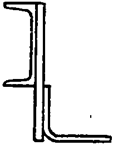
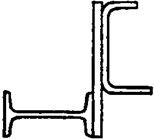
Задание 1 (продолжение)

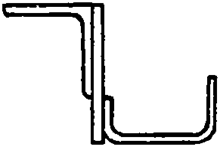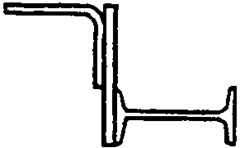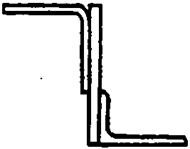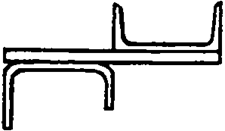Задание 1 (окончание)

Пример решения задачи 1

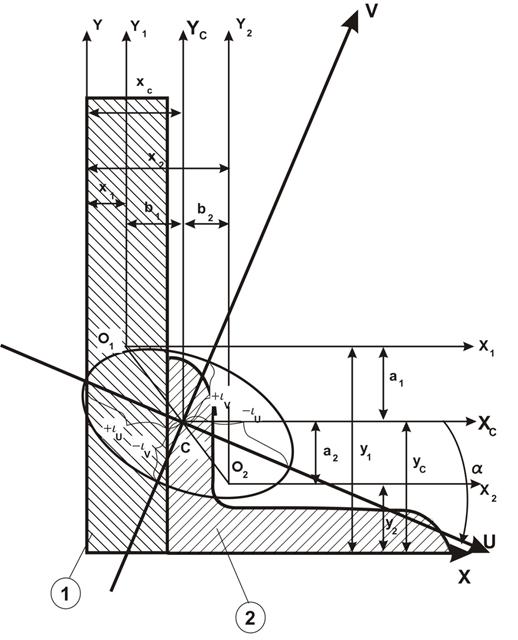
Дано: L

В=14 см, в=9 см, у₀=4,58, х₀=2,12, I_y=145,54 см⁴, I_x=444,45 см⁴, I_u=85,51 см⁴

I_xy=147 см⁴, tqa=0,409, А=22,24см²

Для прямоугольного сечения: h=2 см, в=15 см, А=30 см².

1. Определение координат центра тяжести все сложной фигуры (положение центральных осей)

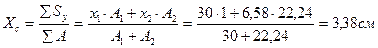
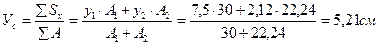
где х₁, у₁; х₂, у₂ – расстояние от центра тяжести каждого сортамента до

вспомогательных осей

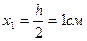
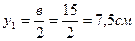
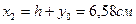
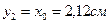
2. Определение осевых моментов инерции относительно центральных осе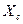й

и

,

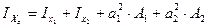
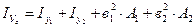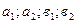- расстояние от центра тяжести каждого сортамента до центральных осей.

Откладываем 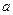по оси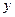

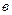по оси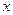

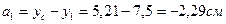
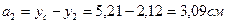
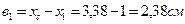
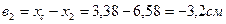
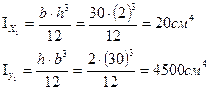
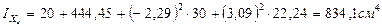
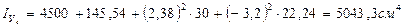
3. Определение центробежного момента инерции относительно центральных осе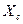й и :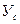

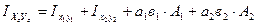
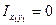, т.к. лист имеет горизонтальную ось симметрии, то собственные центральные оси листа являются главными

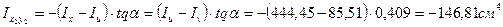
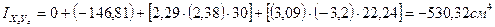
4. Определение моментов сопротивления относительно центральных осей 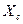и :

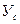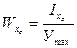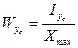; , где

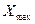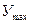, - максимальные расстояния от центра тяжести всей фигуры до наиболее удаленных точек по центральным осям

=

=

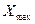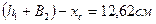
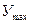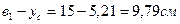
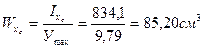
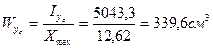
5. Определение положения главных центральных осей угол наклона

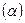
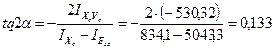
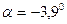, угол откладывается по часовой стрелке

Если угол имеет положительное значение, то откладывается против часовой стрелки.

6. Определение главных центральных моментов инерции относительно главных центральных осей:

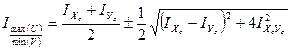
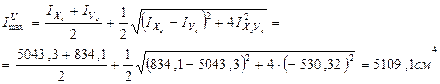
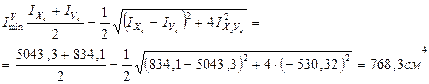
7. Определение моментов сопротивления относительно главных центральных осей :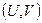

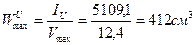
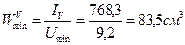
8. Определение радиусов инерции 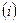относительно центра тяжести:

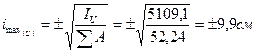
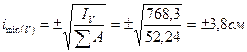
9. Проверка:

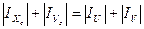
834,1+5043,3=5109,1+768,3

5877,4=5877,4(см⁴)