Данный метод предполагает определение расчетным путем не напряжений, а максимальной нагрузки, которую может выдержать конструкция, не разрушаясь и не претерпевая непрерывно нарастающих пластических деформаций.
При этом в качестве условия прочности необходимо выполнение требования, чтобы наибольшая нагрузка не превышала допускаемого значения, т.е. 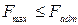
Допускаемая нагрузка, в свою очередь, определяется отношением:
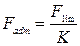
где 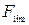 - предельная (разрушающая) нагрузка
- предельная (разрушающая) нагрузка
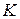 - коэффициент запаса прочности.
- коэффициент запаса прочности.
Нагрузка называется разрушающей, если после ее приложения система утрачивает свою грузоподъемность.
Коэффициент запаса прочности назначается из тех же соображений, что и при расчете по допускаемым напряжениям.
Идею метода расчета по разрушающим нагрузкам высказал в 1904 г. русский ученый и инженер, специалист в области железобетонных конструкций А.Ф.Лолейт.
В основу данного метода положено условие предельного равновесия.
При расчете конструкций из пластичных материалов – это условие, предусматривающее одновременное достижение состояния текучести для всей конструкции в целом.
Площадку текучести имеют диаграммы растяжения малоуглеродистых сталей и некоторых других материалов.
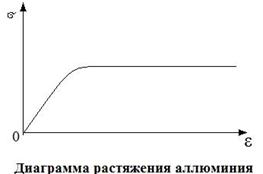
Например, кривая на диаграмме растяжения алюминия (рис.б) за пределом пропорциональности (за пределом действия закона Гука) имеет очень слабый наклон, и при расчетах ее можно принять за горизонтальную прямую.
Для того чтобы упростить расчеты, диаграммы растяжения, сжатия и чистого сдвига для пластичных материалов схематизируют так, что прямая закона Гука непосредственно соприкасается с горизонтальной прямой без плавного перехода
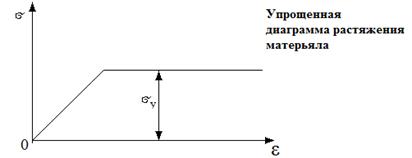
Этим самым принимается равенство между пределами пропорциональности 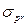 и пределом текучести
и пределом текучести 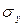 .
.
Длина горизонтального участка диаграммы не ограничивается, т.е. материал считается не упрочняющим, а идеально пластичным. Такая диаграмма называется диаграммой Прандтля.
Указанная схематизация достаточно точна для материалов типа алюминия и вполне допускаема для материалов, имеющих диаграммы с ограниченной площадкой текучести
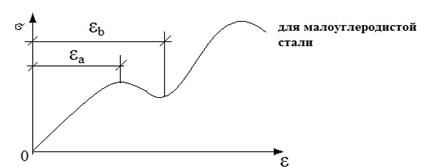
Так, при наличии подобных площадок величина деформации в начале упрочнения 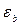 в несколько раз превышает величину деформации
в несколько раз превышает величину деформации 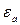 в начале появления пластической деформации.
в начале появления пластической деформации.
Поэтому даже при неравномерном распределении напряжений (изгиб, кручение), но дальнейшем распространении пластической зоны с выравниванием напряжений предела текучести они достигнут одновременно по всему сечению раньше, чем начнется упрочнение материала в точках с наибольшей пластической деформацией.
Таким образом, предельное состояние, обусловленное значительной пластической деформацией, наступит до начала упрочнения материала, и разрушающая нагрузка может быть определена по пределу текучести.
Все теоретические соображения неоднократно проверялись экспериментом, причем, всегда наблюдалось достаточно близкое совпадение величин предельной (разрушающей) нагрузки, определенной экспериментально и расчетным путем.
Условия и порядок выполнения задач
1. Для заданных схем статически определимых балок определить:
· опорные реакции и построить эпюры поперечных сил и изгибающих моментов;
· на эпюрах должны быть проставлены числовые значения величин в характерных точках.
Для каждого участка балки необходимо:
· записать уравнения определяемых величин и вычислить их значения для характерных точек.
2. В задаче 4 дополнительно:
· из условия прочности подобрать стальную балку двутаврового сечения;
· вычислить для этой балки максимальные значения нормального и касательного напряжений;
· в опасных сечениях построить эпюры изменения нормальных и касательных напряжений по высоте двутавровой балки;
· определить прогибы в характерных точках балки (середина пролета, точки приложения сил, крайние точки на консолях);
· по найденным точкам построить изогнутую ось балки. Вычислить также угол поворота сечения на правой опоре.
Чертежи балок выполняются в произвольном масштабе.
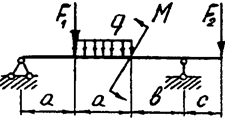
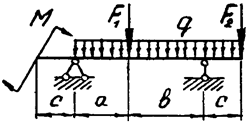
3. В задаче 4а из условия прочности подобрать балку прямоугольного сечения из древесины при отношении высоты к ширине (h:b=4:1). Допускаемое нормальное напряжение для древесины принять равным 10 МПа. Исходные данные (вариант) для решения задач берутся из табл. 4.
Таблица 4
Исходные данные к задаче - 4, 4а, 4б
| Вариант | Заданная нагрузка | Длины участков, м | ||||
| F, кН | q, кН/м | М, кНм | a | в | с | |
| 2,2 | 1,5 | 1,0 | ||||
| 2,4 | 1,6 | 1,1 | ||||
| 2,5 | 1,8 | 1,2 | ||||
| 2,6 | 2,0 | 1,3 | ||||
| 2,8 | 2,1 | 1,4 | ||||
| 3,0 | 2,2 | 1,5 | ||||
| 3,2 | 2,4 | 1,6 | ||||
| 3,4 | 2,5 | 1,7 | ||||
| 3,5 | 2,6 | 1,8 | ||||
| 3,8 | 2,8 | 1,9 |
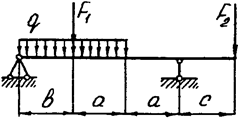
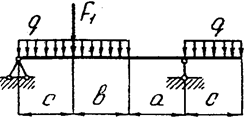
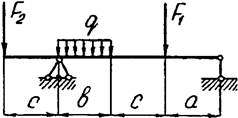
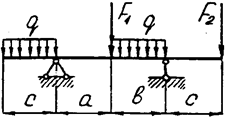
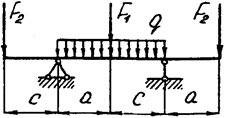
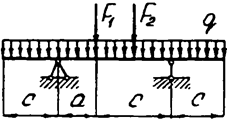
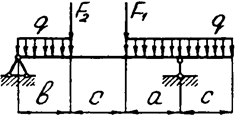
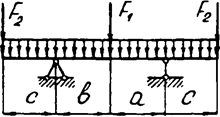
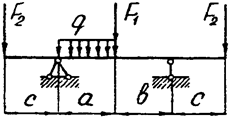
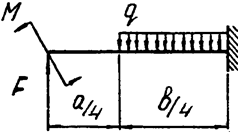
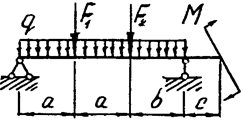
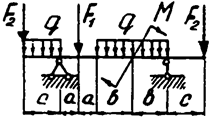
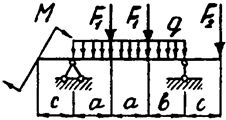
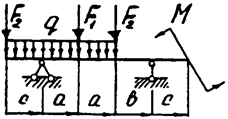
Задача 4. Двухопорная балка
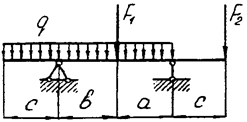 | 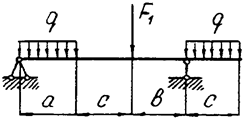 | ||
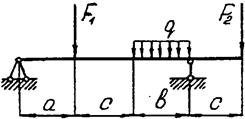 | 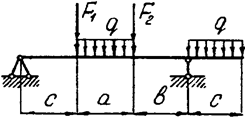 | ||
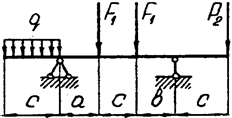 | 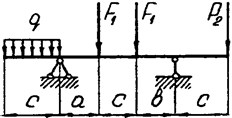 | ||
 |  | ||
 | 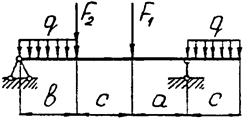 | ||
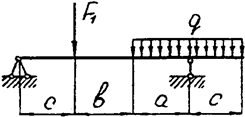
Задача 4 (продолжение)
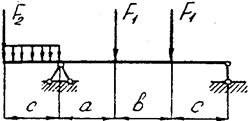 |  | ||
 |  | ||
 |  | ||
 |  | ||
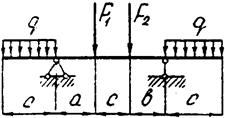 | 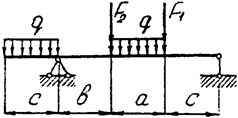 | ||
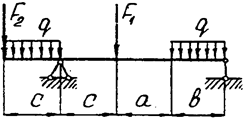
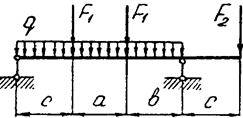
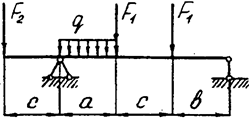
Задача 4 (окончание)
 | 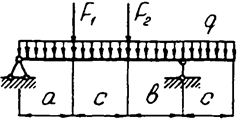 | ||
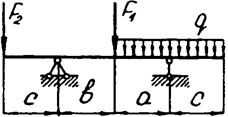 | 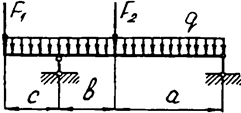 | ||
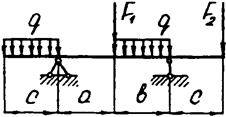 |  | ||
 |  | ||
 | 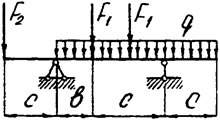 | ||
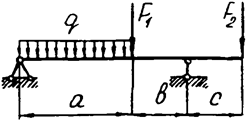
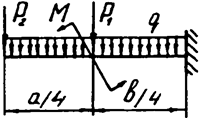
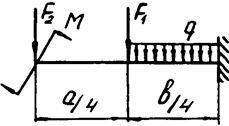
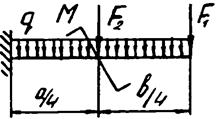
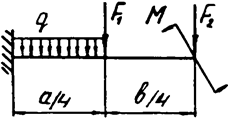
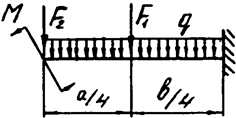
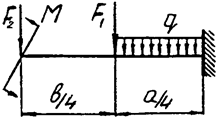
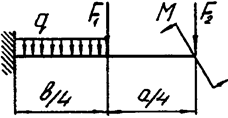
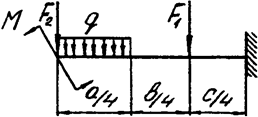
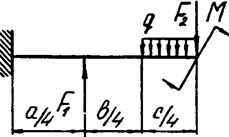
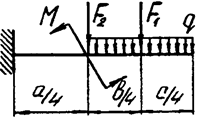
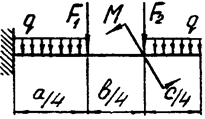
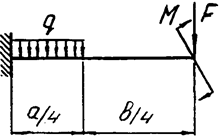
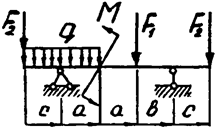
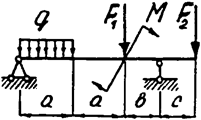
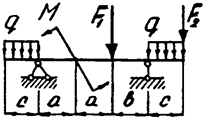
Задача 4а. Консольная балка
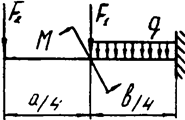 |  | ||
 |  | ||
 |  | ||
 |  | ||
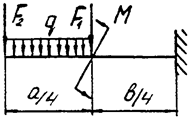 | 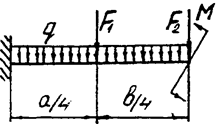 | ||
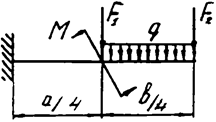
Задача 4а. Консольная балка
 | 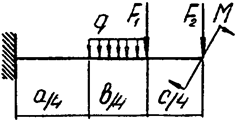 | ||
 |  | ||
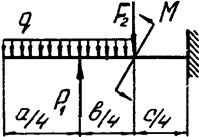 |  | ||
 |  | ||
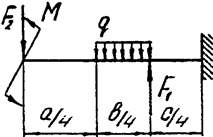 | 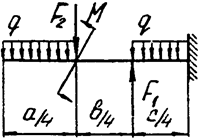 | ||
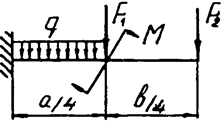
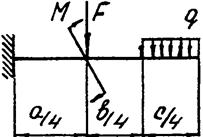
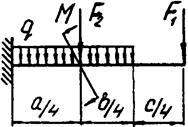
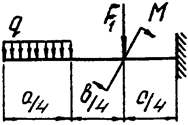
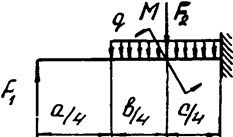
Задача 4а. Консольная балка
 |  | ||
 |  | ||
 |  | ||
 | 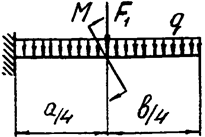 | ||
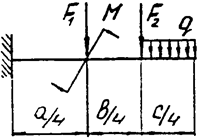 | 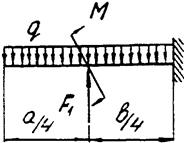 | ||
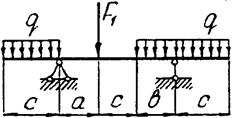
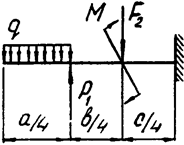
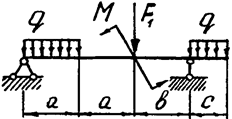
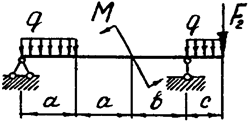
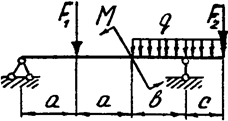
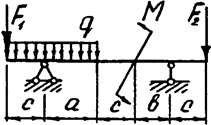
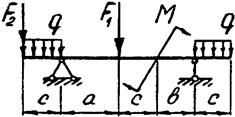
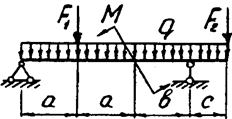
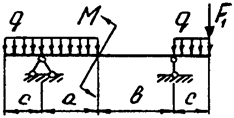
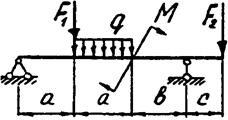
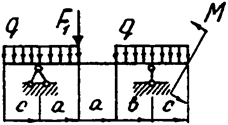
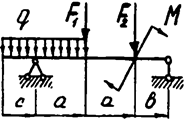
Задача 4б. Двухопорная балка
 |  | ||
 |  | ||
 |  | ||
 |  | ||
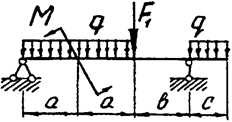 | 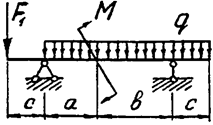 | ||
Задача 4б. Двухопорная балка
 |  | ||
 |  | ||
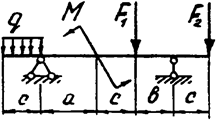 | 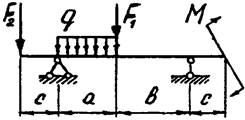 | ||
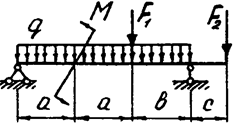 | 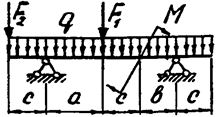 | ||
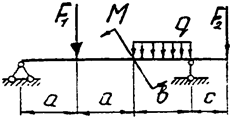 | 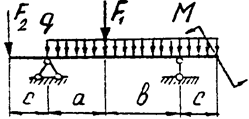 | ||
Задача 4б. Двухопорная балка
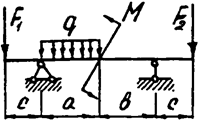 | 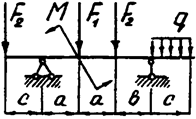 | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
Пример решения задачи 4
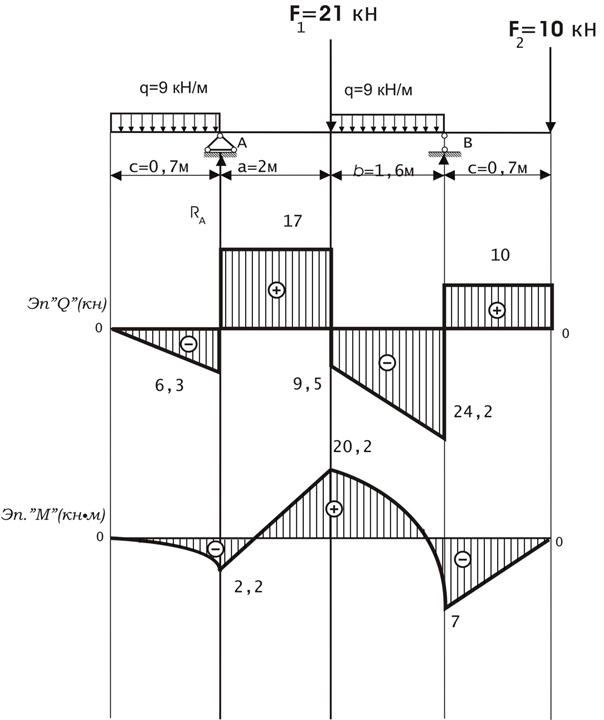
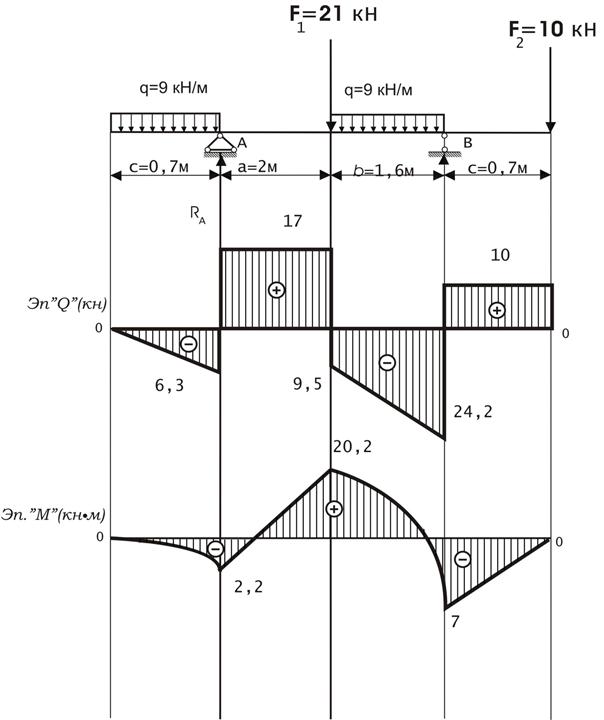
Определить и построить эпюры: крутящих моментов - Мкр, поперечных сил Q, подобрать сечение двутавра.
1. Определение опорных реакций
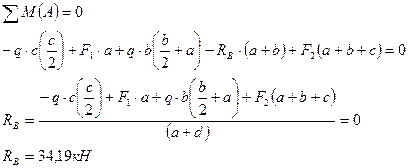
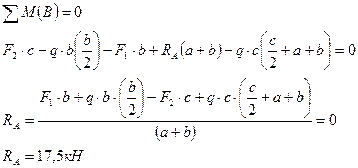
Проверка
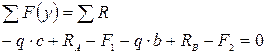
2. Определение внутренних силовых факторов методом сечений
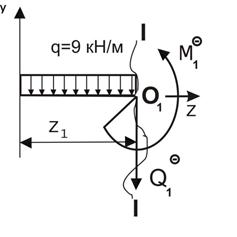 | Сечение I-I 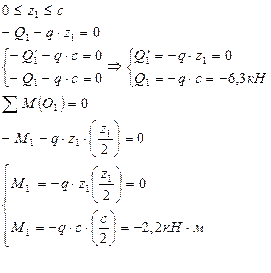 | |
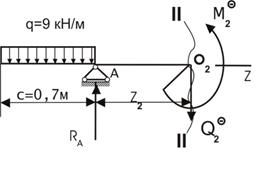 | Сечение II-II 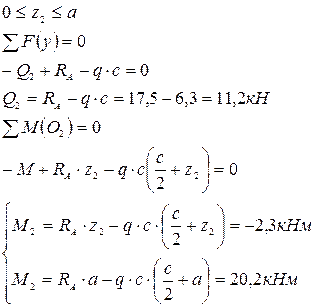 | |
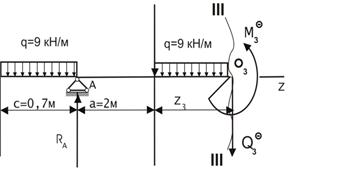 | Сечение III – III 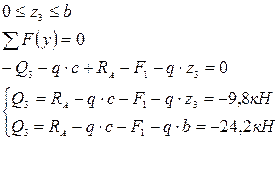 | |
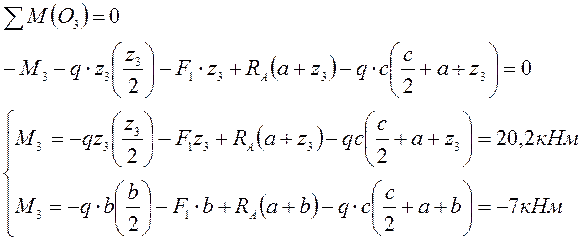 | ||
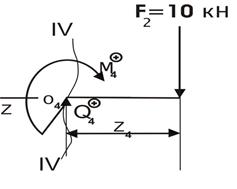 | Сечение IV-IV 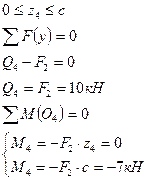 | |
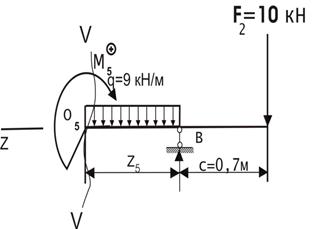 | Сечение V-V 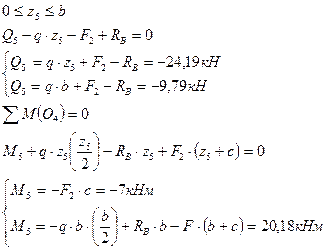 | |
3. Подбор сечения двутавровой балки
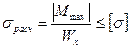 ,
, 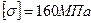
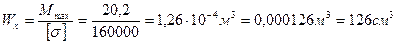
№ 16
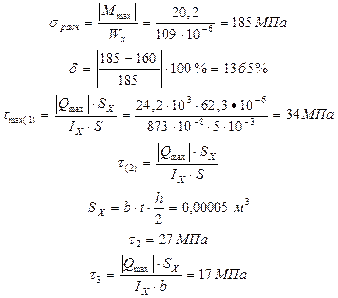
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
 2015-02-24
2015-02-24 8419
8419
