Равномерная сходимость. Критерий Коши равномерной сходимости

Последовательность называется равномерно сходящейся {f(x)} на отрезке [a,b], если для любого ε>0 найдется такая n, зависящая от ε N(ε), что при всех значениях 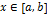и при n>N(ε), выполняется неравенство: |f_n(x)-f(x)|<ε.

Для того, чтобы последовательность функции была равномерно сходящейся на отрезке [a,b], необходимо и достаточно, чтобы ∀ε>0 такой номер, зависящий от ε N(ε), что при номерах n>N(ε) и в любом натуральном числе p неравенство |f_n+p(x)-f_n(x)|<ε выполнялось бы для всех x 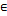[a,b].