Намагниченность. Магнитное поле в веществе

Для количественного описания намагничения магнетиков вводят векторную величину – намагниченность, определяемую магнитным моментом единицы объема магнетика:

,

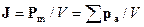где 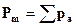- магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул.

Магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Тогда можем записать, что вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля 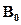(поля, создаваемого намагничивающим током в вакууме) и поля микротоков 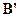(поля, создаваемого молекулярными токами):

,

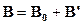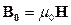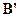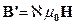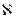где . Так как - вектор намагниченности, и для изотропных магнетиков , где - магнитная восприимчивость.

,

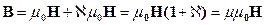здесь 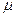- относительная магнитная проницаемость, показывающая, во сколько раз индукция 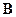магнитного поля в окружающей среде отличается от индукции 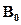в вакууме. Для диамагнетика 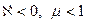, для парамагнетика .

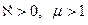Электронный парамагнитный резонанс используется для определения величины 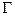. В определенном объеме – резонаторе - находится исследуемое вещество. Образец перемагничивают с частотой 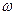, он помещен в магнитное поле 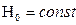. Наблюдают поглощение энергии, которое максимально, если .

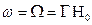Граничные условия:

Рассмотрим границу двух однородных изотропных магнетиков, вдоль которой течет поверхностный ток проводимости с линейной плотностью 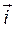. Пусть система находится в однородном магнитном поле. Используем теорему о полном магнитном потоке и теорему о циркуляции вектора напряженност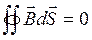и и .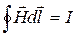

Рассмотрим на границе замкнутую поверхность в виде прямого цилиндра с 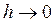(рис.101). Поток вектора магнитной индукции в этом случае: 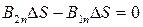или 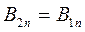, т.е. нормальная составляющая вектора магнитной индукции одинакова в обоих магнетиках. Так как 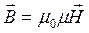, то .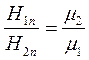

Применим теорему о циркуляции вектора напряженности к очень малому прямоугольному контуру. Пусть вектор линейной плотности тока совпадает с нормалью 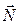к контуру (рис.102).

Так как контур очень узкий, то вклад в циркуляцию на боковых сторонах очень мал. Тогда: 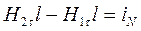, т.е. тангенциальная составляющая вектора напряженности, а следовательно и вектора магнитной индукции на границе раздела претерпевает скачок, обусловленный наличием поверхностных токов проводимости.

Если на границе раздела магнетиков токов проводимости нет, то 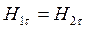и, соответственно, 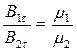. На границе раздела двух магнетиков линии вектора индукции испытывают преломление, но непрерывны .

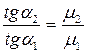Линии вектора напряженности преломляются по такому же закону, но терпят разрыв из-за поверхностных токов намагничивания (даже в отсутствие токов проводимости).

На рис. 103 представлены линии векторов индукции и напряженности для случая > .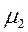

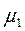На этом основана магнитная защита, т.е. использование замкнутой железной оболочки для защиты внутреннего пространства от внешнего магнитного поля. Линии поля концентрируются в самой оболочке, а в окруженном оболочкой пространстве магнитное поле значительно меньшей величины, чем внешнее поле.