Аналитическая группировка

Аналитическая группировка – распространенный прием статистического изучения связей, которые обнаруживаются при параллельном сопоставлении обобщенных значений признаков по группам. Различают признаки зависимые, значения которых изменяются под влиянием других признаков, их обычно в статистике называют результативными, и факторные, оказывающие влияние на другие. Обычно в основе аналитической группировки лежит признак-фактор, а по результативным признакам производится расчет групповых средних, по изменению величины которых определяют наличие связи между признаками. Таким образом, аналитическими можно назвать такие группировки, которые позволяют установить и изучить связь между результативными и факторными признаками единиц однотипной совокупности.

В качестве признака фактора выберем - численность населения на 1 января 2013 года (млн. чел), а в качестве результата - среднемесячная номинальная начисленная заработная плата работников организации тыс. руб.

Таблица 1.4

Распределение регионов по численности населения на 1 января 2013 года (млн. чел). и среднемесячную номинальную начисленную заработную плату работников организации тыс. руб.

Численность населения	количество регионов	И того по признаку результата	Среднее значение по признаку результата
0.21 - 0.89		2,80	0,46
0.89 - 1.58		10,81	1,20
1.58 - 2.26		5,57	1,85
2.26 - 2.95		18,25	2,6
2.95 - 3.63		13,5	3,37
3.63 - 4.32		4,32	4,32
итого		55,25	13,82

Вывод: Связь между признаками существует, прямая линейная.

Комбинационная группировка

Таблица 1.5

Комбинационная таблица среднемесячной номинальной начисленная з/п и численности населения на 1 янв 2013г

Численность населения на 1 янв 2013г	среднемесячная номинальная начисленная з/п	итого
16,01 - 23,95	23,95 - 31.89	31,89 - 39,83	39,83 - 47,77	47,77 - 55,71	55,71 - 63,70
0.21 - 0.895
0.895 - 1.58
1.58 - 2.26
2.26 - 2.95
2.95 - 3.63
3.63 - 4.32
итого:

На основании полученных данных, можно сделать вывод: максимальные значения расположены не вдоль главной диагонали, значит, между рассматриваемыми признаками не наблюдается явной связи.

Задание 2

2.1 Построение рядов распределения

Ряд распределения – это числовой ряд, который представляет собой упорядоченное распределение единиц статистической совокупности. Он характеризует состав (структуру) изучаемого явления.

Ряд распределения регионов по численности населения на 1 января 2013 года (млн. чел)

Распределение регионов по численности населения на 1 января 2013 года (млн. чел)

Таблица 2.1

Численность населения	количество регионов	в % к итогу	Середины интервалов, хi	Накопленные частоты S
0.21 - 0.89		23,33%	0,55
0.89 - 1.58		26,67%	1,23
1.58 - 2.26		10,00%	1,92
2.26 - 2.95		23,33%	2,6
2.95 - 3.63		13,33%	3,29
3.63 - 4.32		3,33%	5,47
итого		100%

Гистограмма – графическое изображение интервального ряда распределения.

Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.

На основе данных показанных в таблице 2.1 построим гистограмму:

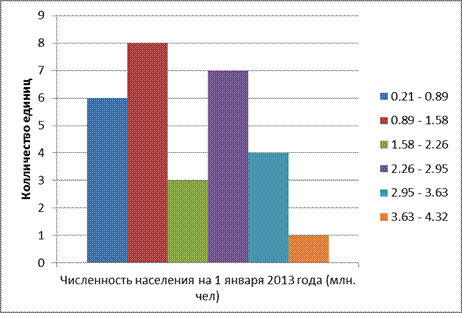
Рис. 1 Гистограмма распределения регионов по численности населения на 1 января 2013 года (млн. чел)

Кумулята – ломаная линия, изображающая ряд накопленных частот. Накопленные частоты наносятся в системе координат в виде ординат для границ интервалов; соединяя нанесенные точки отрезками прямых, получаем кумуляту. Кумуляту называют также полигоном накопленных частот.

На основе данных показанных в таблице 2.1 построим Кумуляту

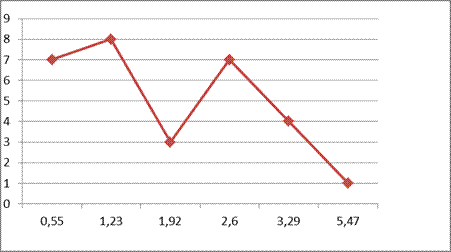
Рис. 2 Кумулятивное распределение по численности населения на 1 января 2013 года (млн. чел)