Следующая логическая операция, которую мы рассмотрим – это операция импликации. Импликация ложна тогда и только тогда, когда 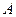 – истинна, а
– истинна, а 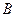 – ложна.
– ложна.
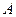
| 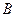
| 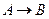
|
Это выражение читается так: если 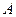 , то
, то 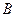 . В таком виде часто формулируются математические теоремы. Если теорема сформулирована как-нибудь иначе, то ее можно перефразировать в указанном виде, не теряя её сущности.
. В таком виде часто формулируются математические теоремы. Если теорема сформулирована как-нибудь иначе, то ее можно перефразировать в указанном виде, не теряя её сущности.
Пример: Теорема: «Вертикальные углы – конгруэнтны» будет выглядеть так: «Если углы вертикальны, то они конгруэнтны». В такой формулировке выявлены посылка – 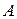 (углы вертикальны) и заключение
(углы вертикальны) и заключение 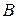 (углы конгруэнтны). Истинность высказывания
(углы конгруэнтны). Истинность высказывания 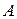 , исключает возможность существования таких углов, которые были бы вертикальны и неконгруэнтны.
, исключает возможность существования таких углов, которые были бы вертикальны и неконгруэнтны.
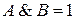 углы вертикальны и конгруэнтны;
углы вертикальны и конгруэнтны;
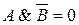 углы вертикальны и неконгруэнтны;
углы вертикальны и неконгруэнтны;
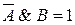 невертикальные углы могут быть конгруэнтны;
невертикальные углы могут быть конгруэнтны;
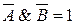 углы могут быть невертикальные и неконгруэнтные.
углы могут быть невертикальные и неконгруэнтные.
В математических терминах импликация еще обозначается фразами:
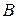 – следствие
– следствие 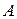 ,
,
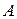 – достаточное условие
– достаточное условие 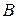 .
.
Импликацию тоже можно выразить через &, Ú, Ø:
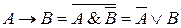 .
.
 2015-02-24
2015-02-24 682
682








