2015-02-24
920
Рассмотрим зацепление двух эвольвентных профиле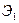й 
и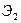 
Рис 5.5, построенных на основных окружностях с радиусам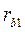и 
и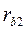 
соответственно.
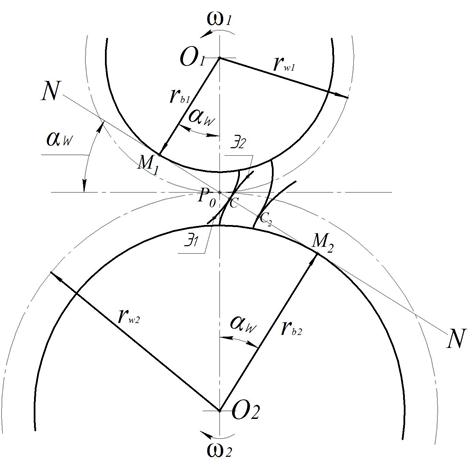
Рис. 5.5
Они касаются, друг друга в точке С. Нормаль N-N к профилям проведенная в точке касания по свойству эвольвенты будет являться касательной к основным окружностям в точках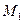 
и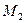 
. При повороте колес точка соприкосновения профилей сместится в точку 
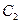, которая так же будет лежать на прямой N-N. Следовательно, в любом положении двух зацепляющихся эвольвент их общая нормаль занимает не изменное положение, что обеспечивает постоянное положение полюса зацепления (точку 
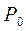). При этом, в соответствии с основным законом зацепления,
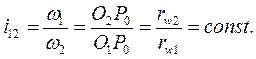
Таким образом, эвольвентное зацепление обеспечивает постоянное передаточное отношение.
Точка контакта (С) перемещается по линии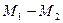 
(линии зацепления), лежащей на нормали N-N. Таким образом, угол 
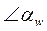- угол зацепления для эвольвентного зацепления остается постоянным и давление одного профиля на другой, передаваемое по нормали N-N, сохраняет постоянное направление.
На величину передаточного отношения не влияют ни угол зацепления, ни межцентровое расстояние так как:
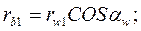
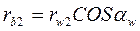
Откуда
,
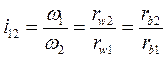То есть передаточное отношение зависит только от радиусов основных окружностей. Поэтому изменение межцентрового расстояния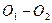 
при изготовлении колес и сборке не влияет на передаточное отношение.
