2015-02-24
2880
Для вывода уравнения эвольвенты окружности рассмотрим Рис 5.4. На этом рисунке обозначим:
- угол развернутости,
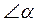- угол профиля,
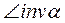- инвалютный (эвольвентный) угол.
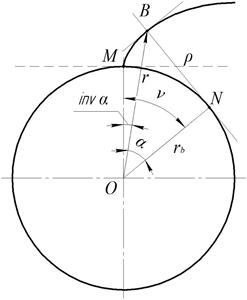
Рис. 5.4
В полярных координатах положение произвольной точки В эвольвенты будет определяться радиусом r 
и полярным углом 
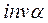. Как видно из Рис 5.4
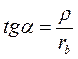
С другой стороны дуга 
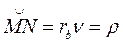
Откуда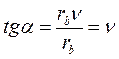 
.
Тогда эвольвентный угол будет
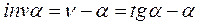(5.4)
Из треугольника ОВМ
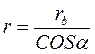(5.5)
Как видно из уравнений (5.4) и (5.5) эвольвента окружности будет определяться радиусом основной окружности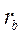 
(параметром), поэтому эти уравнения называются параметрическим и уравнениями эвольвенты.
