Конечность алфавита

Следующее предположение, которое должно быть сделано для основной модели с конечным числом состояний, заключается в том, что каждая переменная может принимать только конечное число различных значений (которые по своей природе могут быть числовыми или не числовыми).

Множество[1] значений, которые переменная v может принимать, называется алфавитом переменной ν и обозначается через V; элемент ν алфавита V называется символом. Пусть K⁽¹⁾, K⁽²⁾,... K^(m) — конечные множества с соответствующими элементами 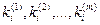и пусть множество 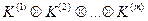обозначает множество всех упорядоченных m -значных наборов (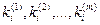). Если входные переменные данной системы суть x⁽¹⁾, x⁽²⁾,..., x^(u), то входной алфавит этой системы, обозначаемый через X, определяется выражением

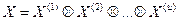, (1.1)

где X⁽ⁱ⁾, i = 1, 2, …, u, - алфавит x⁽ⁱ⁾.

Аналогично, если выходные переменные системы суть z⁽¹⁾, z⁽²⁾,..., z^(w), то выходной алфавит Z системы определяется выражением

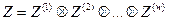, (1.2)

где Z^(j), j = 1, 2,..., w, — алфавит z^(j). Если Х⁽ⁱ⁾ имеет мощность p_i, a Z^(j) мощность q_j, то мощности р для X и q для Z выражается соответственно формулами:

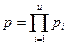, (1.3)

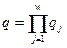, (1.4)

Мощности р и q конечны.

Из определения входного алфавита X видно, что одного символа входного алфавита — входного символа — достаточно для описания всех и входных переменных в любой заданный момент времени t_ν. Аналогично из определения выходного алфавита Z видно, что одного символа выходного алфавита — выходного символа — достаточно для описания всех w выходных переменных в любой заданный момент времени t_ν. Следовательно, входные переменные x⁽¹⁾, x⁽²⁾,..., x^(u) могут быть заменены одной входной переменной х, алфавит которой X определяется выражением (1.1). Выходные переменные z⁽¹⁾, z⁽²⁾,..., z^(w) могут быть заменены одной выходной переменной z, алфавит которой Z определяется выражением (1.2).Соответственно u входных клемм можно заменить одной входной клеммой. В результате получим схематичное изображение, имеющее вид двухклеммного ящика (рис. 1.3), которое является стандартным представлением основной модели конечного автомата.

Для иллюстрации рассмотрим вычислительное устройство, которое имеет две входные линии х ⁽¹⁾ и x ⁽²⁾: по линии х ⁽¹⁾ подаются символы 0 и 1, по линии x ⁽²⁾ — символы 1, 2 и 3.

В произвольные моменты времени t _ν устройство выдает величины 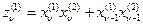и .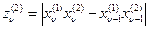

Таким образом, имеем:

X ⁽¹⁾ = {0,1}, X ⁽²⁾ = {1, 2, 3},

Z ⁽¹⁾ = {0, 1, 2, 3, 4, 5, 6}, Z ⁽²⁾={0, 1, 2, 3}

и, следовательно,

X = { (0,1), (0,2), (0,3), (1,1), (1,2), (1,3)},

Z = {(0,0), (0,1), (0,2), (0,3), (1,0), (1,1), (1,2), (1,3), (2,0), (2,1), (2,2), (2,3), (3,0), (3,1), (3,2), (3,3), (4,0), (4,1), (4,2), (4,3), (5,0), (5,1), (5,2), (5,3), (6,0), (6,1), (6,2), (6,3)}