Диагностические эксперименты для двух состояний

Задача определения начального состояния автомата М в случае, когда А (М) имеет произвольную мощность m, конечно, намного сложнее относительно частного случая, когда m = 2. Чтобы различить между собой общий и этот частный случаи, первый будем называть диагностической задачей для т состояний, а второй — диагностической задачей для двух состояний.

В этой главе мы рассмотрим диагностическую задачу для двух состояний, предполагая, что данный автомат М имеет n состояний, с A(M)=(σi₀, σj₀). Так как М минимален, то σi₀ и σj₀ должны быть различимы и, следовательно, (n—1)-различимы. Значит, существует входная последовательность длины n — 1 или менее, которая, будучи приложенной к M|σi₀ и M|σj₀, вызывает различные выходные последовательности. Такая входная последовательность называется диагностической последовательностью для {σi₀, σj₀}.Диагностический эксперимент для двух состояний для автомата М при А (М) = {σi₀, σj₀} состоит, следовательно, в приложении к М диагностической последовательности для {σi₀, σj₀} и в наблюдении реакции; на основании этой реакции может быть определено истинное начальное состояние. В оставшейся части этого параграфа мы покажем, как могут быть построены диагностические последовательности для заданных пар состояний.

Пусть σi₀ и σj₀ будут i-различимы и (l — 1)-эквивалентны, для некоторого l, 1 ≤ l ≤ n - 1[23]. Тогда длина кратчайшей диагностической последовательности для { σi₀, σj₀} есть l. Любая диагностическая последовательность для { σi₀, σj₀}. Длина которой равна определенному выше значению l, будет называться минимальной диагностической последовательностью для { σi₀, σj₀}и обозначаться ε(σi₀, σj₀). Если σi₀ и σj₀ l -различимы и (l -1)-эквивалентны, то σi₀ и σj₀ должны быть разобщенными состояниями в Р _l и объединенными в Р _l-1. Поэтому i может быть определено путем построения k-эквивалентных разбиений для данного автомата М и нахождения наименьшей величины k такой, что P _k содержит σi₀ и σj₀ в двух различных классах; эта величина должна равняться l.

Когда ε(σi₀, σj₀) прикладывается к M|σi₀ и M|σj₀, выходные последовательности получаются одинаковыми, за исключением последнего l -го символа. Следовательно, k-е преемники σi₀ и σj₀ относительно ε(σi₀, σj₀) являются (l — k)- различимыми и (l -k-1) - эквивалентными для всех 0 ≤ k ≤ l — 1. Это положение изображено на рис. 4.2, где ε(σi₀, σj₀) представлена в виде последовательности ξu₁ξu₂... ξu _l. Последовательности состояний, которые проходят автоматы M|σi₀ и M|σj₀ есть соответственно σi₁, σi₂,..., σi_i и σj₁, σj₂,..., σj _{l .} При этом выходные последовательности имеют вид ζ v ₁, ζ v ₂,..., ζ^{( t )} v_l, для автомата M|σi₀ и ζ v ₁, ζ v ₂,..., ζ^{( j )} v_l для автомата M|σi₀, где ζ⁽ⁱ⁾ v_l ≠ ζ^(j) v_l. Используя обозначения рис. 4.2, можно установить, что если σi₀и σj₀ и l -различимы (l — 1)-эквивалентны и если ξu₁ξu₂... ξu _l и есть минимальная диагностическая последовательность для { σi₀, σj₀ }, то: (1) для

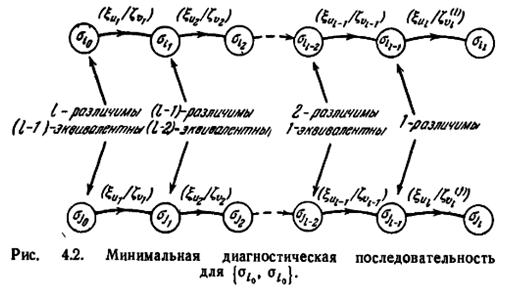
1 ≤ k ≤ l — 1 ξu _k есть входной символ, который переводит σi_k-1 и σj_k-1 в пару (l — k)-различимых и (l—k—1) -эквивалентных состояний σi_k и σj_k; ξu _l есть входной символ, при приложении которого к автоматам M|σi _l-1 и M|σj _l-1 последние выдают различные выходные символы.

Определение ξu _k, σi _k и σj _k из σi _k-1 и σj _k-1 (1 ≤ k ≤ l —1). Определение ξu _k, σi _k и σj _k, когда σi _k-1 и σj _k-1 известны, может быть наиболее удобно произведено с помощью таблиц Р _k, построение которых для эквивалентных разбиений данного автомата описано в § 3.6. σi _k-1 и σj _k-1 выявляются (l — k + 1)-различимыми и (l — k)-эквивалентными состояниями; следовательно, они составляют смежные строки в таблице P _l-k и разобщенные строки в таблице Р _l-k+1. Поэтому строки σi _k-1 и σj _k-1 в таблице Р _l-k должны содержать две клетки, скажем σ´i _k-1 и σ´j _k-1 соответственно, которые имеют различные нижние индексы, по меньшей мере в одном, скажем ξ´u _k-1 -м столбце. При этом σ´i _k-1 и σ´j _k-1 должны быть (l — k—1)-эквивалентными, так как они являются первыми преемниками (l — k)-эквивалентных состояний σi _k-1 и σj _k-1 относительно входного символа ξ´u _k-1; они должны быть также (l —k)-различимыми, так как σ´i _k-1 и σ´j _k-1 имеют различные нижние индексы в таблице P _l-k. Следовательно, σ´i _k-1 и σ´j _k-1 являются искомыми состояниями σi _k и σj _k соответственно, и входной символ ξ´u _k-1 есть искомый входной символ ξu _k. Таким образом, ξu _k, σi _k и σj _k могут быть определены путем просмотра таблицы P _l-k.

Определение ξu _l из σi _t-1 и σj _l-1. σi _t-1 и σj _l-1. являются 1-различимыми; поэтому должен существовать, по крайней мере, один входной символ, при приложении которого к автоматам M|σi _l-1 и M|σj _l-1 последние выдают различные выходные символы. Этот символ, который является искомым символом ξu _l, может быть легко определен путем нахождения в z _v -подтаблице столбца, в котором строки σi _t-1 и σj _l-1 различны.

Приведенные методы могут быть объединены и представлены в виде следующего алгоритма.

Алгоритм 4.1. σi ₀ и σj ₀ суть два состояния автомата М. Чтобы определить минимальную диагностическую последовательность для { σi ₀,σj ₀ }: (1) Построим таблицы P _k для М. Найдем l такое, что σi ₀ и σj ₀, являются смежными строками в таблице P l -1 и разобщенными строками в таблице Р _l. Предположим, что k=1. (2) (а) Если l — k > 0, то переходим к шагу 3. (б) Если l — k = 0, то ξu _k соответствует любому столбцу в z _v -подтаблице М, такому, что строки σi _k-1 и σj _k-1 в этом столбце различны. ξu₁ξu₂... ξu _k есть минимальная диагностическая последовательность для { σi ₀, σj ₀ }. (3) ξu _k соответствует любому столбцу в таблице P l -k, такому, что строки σi _k-1 и σj _k-1 этого столбца имеют клетки σi _k и σj _k соответственно с различными нижними индексами. Увеличиваем k на единицу и возвращаемся к шагу (2).

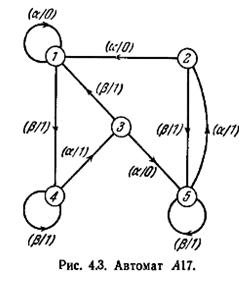
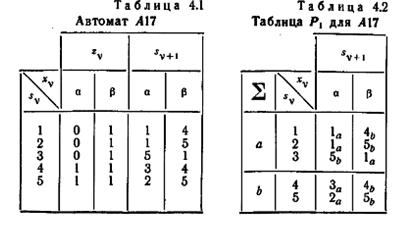
Для иллюстрации рассмотрим автомат A17, представленный таблицей 4.1 и изображенный на рис. 4.3. Таблицы 4.2 — 4.5 являются таблицами P_1, Р₂, Р₃ и Р₄ автомата A17. Для примера найдем минимальную диагностическую последовательность для {1,2}, т. е. ε(1,2). Начнем с рассмотрения таблицы Р₃, так как это «последняя» таблица, в которой строки 1 и 2 являются смежными. Строки 1 и 2 в таблице Р₃ имеют различные нижние индексы в клетках «4_c» и «5_d», которые находятся в столбце β. Значит, β есть первый символ в ε(1,2). В таблице Р₂ строки 4 и 5 имеют различные нижние индексы в клетках «З_b» и «2_а», которые находятся в столбце а. Значит, а есть второй символ в ε(1,2). В таблице Р₁ строки 3 и 2 имеют различные нижние индексы в клетках «5_b» и «1_а», которые находятся в столбце а. Значит, а есть третий символ в ε(1,2). Β также может быть выбран в качестве третьего символа, так как строки 3 и 2 имеют различные нижние индексы в клетках «1_а» и «5_b», которые находятся в столбце β. В z _v -подтаблице строки 1 и 5 имеют различные клетки (0 и 1) в столбце а. Значит, а есть четвертый и последний символ в ε(1,2). Таким образом, ε(1,2) имеет

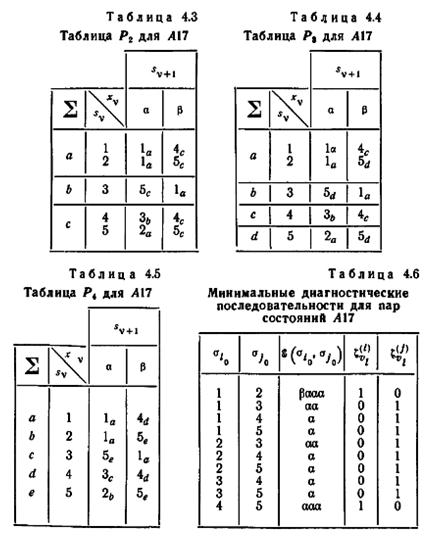
вид β aaa или β a β a. Когда β aaa прикладывается к A17 в состоянии 1 и в состоянии 2, последний выходной символ есть 1 и 0 соответственно, что легко может быть проверено по таблице 4.1 или по рис. 4.3. Следовательно, если {1,2} является множеством допустимых начальных состояний A17, то диагностический эксперимент может быть проведен путем приложения β aaa и наблюдения последнего выходного символа: если этот символ—1, то начальное состояние — 1, если этот символ—0, то начальное состояние — 2. В таблице 4.6 перечислены все минимальные диагностические последовательности для всех пар состояний { σi ₀, σj ₀ } A17; последние два столбца в этой таблице указывают последние наблюдаемые выходные символы ζ⁽ⁱ⁾ v₁ и ζ^(j) v₁, когда минимальная диагностическая последовательность прикладывается к σi ₀ и σj ₀ соответственно. Хотя для данной пары состояний могут быть построены две или более минимальных диагностических последовательностей, в таблице приведена только одна такая последовательность.