Диагностическое дерево

Дерево преемников, определенное в предыдущем параграфе, по своему протяжению бесконечно и как таковое не имеет практического применения. В этом разделе мы дадим определение «усеченного» варианта дерева преемников путем формулировки ряда «правил завершения». Правило завершения определяет, когда ветвь может быть оставлена в качестве оконечной ветви, т. е. ветви, которая не порождает каких-либо ветвей следующего уровня.

Следующие правила завершения определяют структуру, которую будем называть диагностическим деревом.

Определение 4.1. Диагностическое дерево есть дерево преемников, в котором ветвь b k-гo уровня становится

оконечной, если удовлетворяется одно из следующих условий: (1) A-группа, связанная с b, содержит кратное σ -множество. (2) A-группа, связанная с b, связана с некоторой ветвью уровня, предшествующего k-му. (З) Имеется ветвь k-го уровня (возможно, сама ветвь b), связанная с простой A-группой.

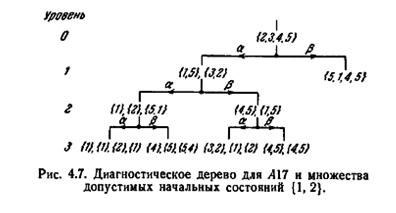
Условие (3) подразумевает, что первый уровень, который содержит ветвь, связанную с простой A-группой, является также последним уровнем в диагностическом дереве. Дерево, последний уровень которого является k-м, называется деревом высоты k. Рис. 4.7 показывает, как строится диагностическое дерево для автомата A17, представленного на рис. 4.3, и для множества допустимых начальных состояний {2, 3, 4, 5}. Ветвь первого уровня, связанная с A-группой {5, 1, 4, 5), является оконечной в силу правила (1). Очевидно, что на третьем уровне A-группа {1}, {1}, {2}, {1} является простой; поэтому в силу правила (3) все ветви на третьем уровне являются оконечными. В качестве другого примера на рис. 4.8 показано диагностическое дерево для A17 и множества допустимых начальных состояний {1, 2}. Ветвь первого уровня, связанная с A-группой {1, 1}, является оконечной в силу

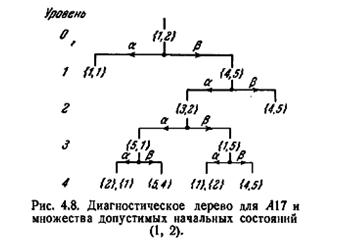
правила (1). Ветвь второго уровня, связанная с A-группой {4, 5}, является оконечной в силу правила (2), так как эта A-группа уже связана с ветвью первого уровня. Очевидно, что в четвертом уровне A-группа {2}, {1} является простой; поэтому в силу правила (3) все ветви на четвертом уровне являются оконечными.

Лемма 4.4. Высота диагностического дерева, построенного для автомата M с n состояниями и множества допустимых начальных состояний мощности m, определяется величиной h, где

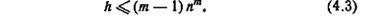
Доказательство. Пусть A-группа G состоит из σ -множеств g₁, g₂,.., g_r, где мощность g_i есть m_i. Множество чисел m₁,m₂,..., m_r, называется распределением размещения G. Число различных A-групп, имеющих то же распределение размещения, что и G, может достигать

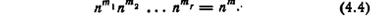
Теперь, если А(М) обозначено через G₀, a G_k есть A-группа, связанная с k-й ветвью пути по дереву, то либо распределение размещения для G_k такое же, как для G_k-1, либо, по лемме 4.1, решение G_k превышает решение G_k-1. Следовательно, если G_j, G_j+1,..., G_j+n^m_-1 различны и имеют одинаковое решение r, то G_j+n^m должно быть либо тождественным с одной из предыдущих A-групп, либо иметь решение r'≥r+1. По индукции, число последовательных A-групп с решением r или меньшим таких, что никакие две группы не одинаковы, составляет, как максимум, rn^m. В частности, число последовательных A-групп с решением m — 1 или менее таких, что никакие две группы не одинаковы, достигает (m — 1)n^m. Следовательно, если G₀, G₁,..., G_(m-1)n^m_-1 различны и не просты, то G_(m-1)n^m должна либо быть одинаковой с одной из предшествующих A-групп, либо быть простой. Таким образом, путь, который не заканчивается на [(m — 1)n^m]-й ветви в силу правила (2), должен заканчиваться на этой ветви в силу правила (3). Следовательно, никакой путь в диагностическом дереве не может состоять из более чем (m — 1)n^m ветвей, и тем самым лемма доказана.

Во всех конкретных случаях h существенно меньше, чем граница, выраженная формулой (4,3), так как в формулу (4.3) мы не включили влияние правила (1) на длину пути или влияние на длину пути A-групп, связанных с другими путями. Лемма 4.4 доказывает, по крайней мере, что число уровней в диагностическом дереве конечно и что поэтому построение такого дерева представляет собой конечный процесс.

Диагностическим путем будем называть любой путь в диагностическом дереве, оконечная ветвь которого связана с простой A-группой. Диагностической последовательностью для М и A (М)= (σi₁, σi₂,.., σi_m) будем называть любую входную последовательность, которая, будучи приложена к М|σi₁, М|σi₂,..., М|σi_m, дает в результате m различных выходных последовательностей. Тогда из леммы 4.2 следует

Лемма 4.5. Входная последовательность, описанная диагностическим путем в диагностическом дереве, построенном для М и A (Ж), есть диагностическая последовательность для М и A(M).

Минимальная диагностическая последовательность для М и А(М), обозначаемая через ε (A), есть кратчайшая диагностическая последовательность для М и А(М). Усеченные пути диагностического дерева, построенного для М и А(М), представляют собой пути, имеющиеся в дереве преемников, но отсутствующие в диагностическом дереве в силу правила (1) или (2).

Лемма 4.6. Усеченные пути диагностического дерева, построенного для М и А(М), не описывают минимальных диагностических последовательностей.

Доказательство. Если путь усечен в силу правила (1), то он оканчивается некоторой ветвью b, связанной с A-группой, которая содержит кратное а-множество. По лемме 4.1, каждый путь, проходящий через b в дереве преемников, должен приводить к A-группе, которая содержит кратное σ -множество. Следовательно, такой путь не может вести к простой A-группе и потому не может быть диагностическим путем. Рассмотрим теперь усеченный в силу правила (2) путь, оканчивающийся на j-м уровне ветви b_j, которая связана с A-группой G. Тогда должна существовать ветвь b_i i-го уровня, где i < j, также связанная с G. По лемме 4.3, если в дереве преемников простая A-группа может быть достигнута из b_j через j ветвей, то простая A-группа также может быть достигнута из b_i через i ветвей. Следовательно, если в дереве преемников диагностический путь проходит через b_j, то через b_i должен также проходить диагностический путь; кроме того, последний должен быть более коротким, чем предыдущий, так как i < j. Следовательно, если дерево преемников содержит диагностический путь, который проходит через b_j, то этот путь не может быть описан минимальной диагностической последовательностью.

Теорема 4.2. Множество последовательностей, описываемых диагностическими путями в диагностическом дереве, построенном для автомата М и множества допустимых начальных состояний А (М), представляет собой множество всех минимальных диагностических последовательностей для М и для А (М). Доказательство. По лемме 4.6 множество диагностических путей, представляемых диагностическим деревом, должно содержать пути, которые описывают все минимальные диагностические последовательности для М и А(М). Так как в силу правила (3) все диагностические пути, представляемые деревом, имеют одинаковую длину, то все они должны быть минимальными. Если диагностическое дерево не представляет диагностических путей, то все эти пути оканчиваются в силу правил (1) и (2), и, следовательно, по лемме 4.6, для М и A (M) не существует диагностической последовательности.