Разновидности диагностической задачи с двумя состояниями

Следующая теорема суммирует рассуждения, приведенные в предыдущем параграфе.

Теорема 4.1. Диагностическая задача для автомата, содержащего п состояний, с двумя допустимыми состояниями всегда может быть решена простым безусловным экспериментом длины

l, где l ≤n -1. (4.1)

Рис. 4.4, на котором изображен автомат A18, показывает, что верхняя граница в соотношении (4.1) может быть до-

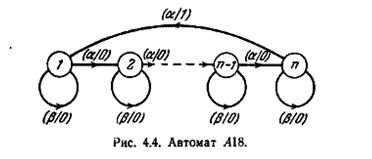
стигнута для любого n. Очевидно, что в A18 никакие два состояния не могут выдать различные выходные символы прежде, чем будет достигнуто состояние n из одного из этих состояний и приложен входной символ а; следовательно, Диагностический эксперимент для A18 и допустимого множества {1,2} не может быть короче, чем n—1. Минимальная диагностическая последовательность для {1, 2} состоит из последовательности n — 1 символов а, выходная последовательность оканчивается нулем, если начальное состояние —1, и единицей, если начальное состояние —2.

Диагностическая задача для двух состояний прямо связана со следующей задачей: известно, что данный автомат М является либо автоматом М₁ в состоянии σ _i, либо автоматом М₂ в состоянии σ _j, причем имеются таблицы переходов М ₁, М₂

и М ₁, М₂ являются сравнимыми автоматами. Желательно распознать автомат и его начальное состояние. Простым искусственным приемом рассмотрения М как расщепляемого автомата М ₁ и М₂, а именно ∆(М ₁, М₂), указанная задача может быть перефразирована в следующем виде: известно, что данный автомат ∆(M₁, M₂), таблица переходов которого доступна, находится в одном из состояний {σ _i, σ _j }. Найти это состояние. Эта задача в точности представляет собой диагностическую задачу для автомата ∆(M₁, M₂) и допустимого множества начальных состояний {σ _i, σ _j }. При σ _i≠ σ _j задача может быть решена методом, описанным в § 4.4. По теореме 4.1, мы имеем:

Следствие 4.1. Известно, что данный автомат должен быть либо M₁ в состоянии σ _i, либо М ₂ в состоянии σ _j, где σ _i≠ σ _j, М₁ и М₂ сравнимы и их таблицы переходов доступны. Если М₁ есть автомат с n₁ состояниями, а М₂ — с n₂ состояниями, то данный автомат и его начальное состояние всегда могут быть установлены простым безусловным экспериментом длины l, где

l ≤ n₁+n₂ -1 (4.2)

Как показано на примере автоматов A19 и A20 (рис. 4.5), верхняя граница в соотношении (4.2) может быть достигнута в точности для любых n₁ и n₂. В примере предполагается, что n₂ ≥ n₁ (когда n₁=n₂, состояние n₁ в A20 имеет единственную исходящую дугу, отмеченную (а /0) V (β/0). которая ведет к состоянию n₁ — 1). Прежде всего заметим, что никакие два состояния i в автомате A19 и j в автомате A20 не могут выдать различных выходных символов до тех пор, пока не будет достигнуто состояние 1 из i и j и не будет приложен входной символ β. Далее, вычеркнем в A20 пару вход-выход (а /0) исходящей из состояния n ₂ дуги, обозначенной (а /0) V (β/0). добавим к n₂ петлю (а /0) и рассмотрим,

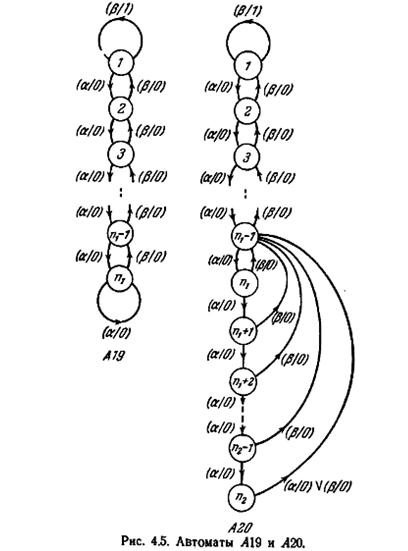
как это повлияет на A20. Как только это сделано, состояния n₂ и n₂ — 1 становятся явно эквивалентными и могут быть заменены одним состоянием, скажем n₂ — 1; состояния n₂—1 и n₂ — 2 являются теперь явно эквивалентными я также могут быть заменены одним состоянием, скажем n₂— 2;...; состояния n₁+1 и пх являются теперь явно эквивалентными и могут быть заменены одним состоянием, скажем n₁. В своей сокращенной форме автомат A20 одинаков с A19 и, следовательно, состояние i A19 эквивалентно состоянию i A20 для всех i, l ≤i≤n_j. Поэтому можно сделать вывод, что кратчайшая входная последовательность, под действием которой A19 и A20 должны выдавать различные выходные /последовательности, когда оба автомата находятся в начальном состоянии 1, должна переводить автомат A20 из состояния 1 в состояние n₂ и затем входным символом а в состояние n₁ — 1. Так как состояние 1 должно быть вновь достигнуто перед тем, как либо A19, либо A20 выдадут различные выходные символы, та же самая последовательность должна переводить A20 из состояния n₂ в состояние 1 и затем оканчиваться входным символом β. Поэтому кратчайший эксперимент, различающий между собой A19 в состоянии 1 и A20 в состоянии 1, состоит в приложении n₂ символов а, за которыми следуют n₁ — 1 символов β, c общей длиной n₁ + n₂ — 1. Последний аблюдаемый символ в этом эксперименте есть 0, если в состоянии 1 находится автомат A19, и 1, если в состоянии 1 находится A20.

Следует отметить, что единственное требование, предъявляемое к M₁ и М₂ в следствии 4.1, состоит в том, что σ _i≠ σ _j. Это требование не зависит от различимости или эквивалентности М₁ и М₂ (σiи σj могут быть различимыми состояниями в двух эквивалентных автоматах). Следовательно, нет необходимости распространять на расщепляемый автомат ∆(M₁, M₂) предположение о том, что отдельные автоматы М₁

и М₂ являются минимальными.