Доказательство. Т.к. f(x) /g(x) => f(x)= g(x)×h(x), где h(x) ÎP[x]

Т.к. f(x) /g(x) => f(x)= g(x)×h(x), где h(x) ÎP[x]

Т.к. g(x) /f(x) => g(x)=f(x)×s(x), где s(x) ÎP [x]

f(x)=f(x)× 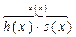=> f(x) = f(x)×u(x) => cm u(x)=0 => u(х) = с,

где с Î Р, т.е. f (x)=g(x)c. Многочлены f(x) и g(x) называют ассоциированными.

Свойство 4. Если (f(x) / g(x)) & h(x) Î P => (f(x)×h(x)) / g(x). Докажите это свойство самостоятельно.

§3. Деление с остатком в кольце P[x].

Определение 1. Многочлен f(x) Î P[x] делится на многочлен g(x) ¹ 0 из этого же кольца с остатком, если $h(x) и r(х) из Р[х]: f(x)= g(x) h(x)+r(x), где cm r(x) <cm g(x) Ú r(x) = 0.

Теорема 1. Для любой пары многочленов f(x) и g(x) из кольца Р[х], где g(x) ¹ 0, $! пара многочленов h(x) и r(х) из

Р[х]: f(x)=g(x) h(x)+r(x), причём cm r(x) < cm g(x) Ú r(x)=0