Пример 2 Глава 6. Теория делимости в кольце Р[х]

Каноническое разложение числа 588000 = 2⁵×3×5³×7²

Следствие 1. Если 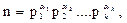тогда все делители числа (n) имеют вид: 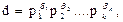где 0£b_i£a_i (i = 1, 2,…,k).

Пример 3. Все делители числа 720 = 2⁴×3²×5 получим, если в выражении 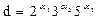вместо a₁, a₂, a₃, независимо друг от друга, будем подставлять значения: a₁=0, 1, 2, 3, 4, a₂=0, 1, 2, a₃ = 0, 1.

Искомые делители будут равны: 1; 2; 4; 8; 16; 3; 6; 12; 24; 48; 9; 18; 36; 72; 144; 5; 10; 20; 40; 80; 15; 30; 60; 120; 240; 45; 90; 180; 360; 720.

Следствие 2. Есл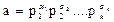и и 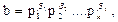то (a, b) = p₁^l1 p₂^l2 …p_k^lk, где li = min(a_I, b_i)

[a, b] = p₁^d1 p₂^d2 …p_k^dk , где di = max(a_I, b_i).

Пример 4. Найти НОД(a, b) и НОК(a, b), используя каноническое разложение, если

a = 24, b = 42.

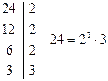
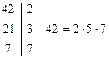
(24, 42) = 2×3 = 6

[24, 42] = 2³×3×7 = 168

Глава 6. Теория делимости в кольце Р[х].

В процессе изучения этой темы студенты должны овладеть следующими знаниями, умениями, навыками:

- знать определение многочлена f(x) нал полем Р;

- уметь строить кольцо многочленов <Р[х], +, •> и линейное пространство < Р[х], + {wl, l Î R} >, знать его базис,

размерность и их свойства;

- знать отношение делимости в кольце Р[х];

- знать и уметь находить HOK(f, g) и НОД (f, g) различными способами;

- знать методы нахождения корней многочлена в поле R, С и Q;

- уметь разложить многочлен на неприводимые множители над полем R, С и Q;

- знать формулы Виета, «схему Горнера», уметь их использовать в процессе решения разного типа задач.

§1. Построение кольца Р[х].

Пусть дано произвольное поле Р, его элементы будем обозначать а₁, а₂,..., а_n...

Определение 1. Многочленом n - й степени от одной переменной называют выражение вида: а_nхⁿ + а_n-1x^n-1 +...+ a₁x+a₀, где а_iÎР, а_n ¹ 0, n Î N⁰ = N È {0}.

Замечание. а_iхⁱ - называют членом многочлена; i - степенью этого члена (если а_i ¹ 0); а_i - коэффициентом многочлена и соответствующего члена. Если а_i = 0, то члену а_iхⁱ не приписывается никакой степени, а₀х⁰ - член нулевой степени, если а₀ ¹0 - элемент поля Р.

Для краткой записи многочленов используют знаки f(x), g(x), h(x) и т.п.

Определение 2. Многочлен f(x)= 0хⁿ + 0х^n-1 +...+ 0х + 0 называют нуль-многочленом. Его степень также не определяется.

Определение 3. Степенью многочлена f(x)называют наивысшую из степеней его членов.

Например, f(x)=x³ + 3х⁷ + 4х² + 2, cт f (x) = 7.

Из определений (1-3) следует, что всё множество многочленов Р[х] = {f(x)| f(x) = a_nxⁿ+...+ ax + а₀} можно разбить на три класса:

1. нуль-многочлен f(x)=0xⁿ+... +0х+0;

2. многочлены нулевой степени (а_i Î Р);

3. многочлены степени выше нулевой f(x), g(x)...

Если даны два многочлена f(x) и g(x), то всегда можно считать, что они содержат одинаковое число членов, т.к. недостающие члены всегда можно приписать с нулевыми коэффициентами, например:

f(x) = х⁵ - х⁴ + 2x³ + 3х² - 5х + 1

g(x) = 0х⁵ - 0х⁴ + 3х³ + х² - 0х + 5

Понятие степени позволяет задать отношение порядка на множестве многочленов P[x]:

а) либо в порядке возрастания степени их членов, например:

f(х) = 3+4х²-5х⁴ + х⁶;

б) либо в порядке убывания степени их членов, например:

f(х) = Зх⁵-х³ + 2х² + 8;

Всё вышесказанное позволяет определить понятие алгебраического равенства двух многочленов.

Определение 4. "f(x), g(x) Î P[x], если

f(x) = a_nxⁿ+a_n-1 x^n-1+...+ а₁x+ а₀ и

g(x) = b_nхⁿ+b_n-1 х^n-1+…+b₁+b₀, то

f(x) = g(x) Û (а_n = b_n) & (a_n-1 = b_n-1)&... & (a₀ = b₀)

Это отношение будет:

а) рефлексивно, т.к. "f(x), f(x)= f(x);

б) симметрично, т.к. "f(x), g(x), если (f(x)= g(x)) Þ (g(x)= f(x));

в) транзитивно, т.к. "f(x), g(x), h(x), если [f(x)=g(x)]&[g(x)=h(x)] => [f(х) = h(x)]. (Проверьте!)

Таким образом, отношение равенства многочленов есть отношение эквивалентности на множестве Р[х], в каждый класс эквивалентности попадает только один многочлен.

Замечание. Выше мы определили понятие многочлена как некоторое формальное выражение, однако понятие многочлена можно определить и с других точек зрения. Например, многочлен f(x) = a_nxⁿ+a_n-1 x^n-1+...+ а₁x+ а₀ можно рассматривать как арифметический вектор (а₀, a₁, a₂,...,a_n, 0...0), т.к. коэффициенты многочлена определяют его однозначно. Так, по вектору (3, 5, 1) можно составить многочлен f(х)= х² + 5х + 3.

С другой стороны, многочлен f(x) можно рассматривать как некоторую функцию, определённую на множестве Р. Поэтому отношение равенства двух многочленов каждый раз определяется по-новому (как равенство двух арифметических векторов и как равенство двух функций).

Определим на множестве Р[х] три операции:

1. "f, g Î P[x], f + g = (a_n + b_n)xⁿ + (a_n-1 + b_n-1)x^n-1 +...+ (a₀ + b₀)

2. "f Î P[x], "lÎP, lf=la_nxⁿ +la_n-1x^n-1+…+la₁x +la₀

3. "f, gÎP[x], f×g = a₀b₀ + (a₀b₁ + a₁b₀)x+…+(a₀b_i +...+ a_ib_i-1 + a_ib₀)xⁱ + +... + a_nb_mx^n+m

Замечание. Из этих определений следует, что действия сложения и умножения - это бинарные операции, действие умножения на скаляр при фиксированном l, будет унарной операцией.

Пример 1. Пусть f(x) = 3х⁵ - 2х³ + 4, g(x) = 2х⁴ + х² + 1, тогда

f(x) + g(x) = 3х⁵ + 2х⁴ + 2х³ + х² + 5

f(x) • g(x) = (3х⁵ + 2х³ + 4)(2х⁴ + х² + 1) = 6х⁹ + 3х⁷ + 3х⁵ + 4х⁷ + 2х⁵ + 2х³ + 8х⁴ + 4x² + 4 = 6х⁹ + 7х⁷ + 5х⁵ + 8х⁴ + 2x³ + 4х² + 4

3 • g(x) = 6х⁴ + Зх² + 3

Свойства степени многочлена вытекают из определения операций:

1. свойство Если f(x) ¹ 0 и g(x) ¹ 0, то

cm(f(x) + g(x)) £ max(cm f(x), cm g(x))

2. свойство Если f(x) ¹ 0 и g(x) ¹ 0,то cm (f(x)×g(x)) = cm f(x) + cm g(x)

Действительно, это следует из определения операции умножения и того, что если cm f(x) = n, значит а_n ¹0, если cm g(x) = m, значит b_m ¹ 0, тогда а_n×b_m ¹ 0 т.к. а_n,b_m Î P, а в поле делителей нуля нет. Поэтому член а_n×b_mx^m+n многочлена f(x)×g(x) будет иметь наивысшую степень (m+n).

Это свойство позволяет сделать вывод, о том, что множество многочленов не содержит делителей нуля.

Теорема 1. Алгебра <Р[х], +, •> - является коммутативным, ассоциативным кольцом с единицей.

Доказательство.

I. Нужно проверить, что множество Р[х] - множество многочленов, замкнуто относительно указанных операций

II. Проверить выполнение следующих аксиом:

1. " f, g Î P[x], f + g = g + f

2. " f, g, h Î P[x], (f + g) + h = f + (g + h)

3. $ 0 Î P[x]: " f Î P[x], 0 + f = f + 0 = f

4. "f Î P[x] $ (-f) Î P[x]: f + (-f) = (-f) + f = 0

5. " f, g, h Î P[x], (f + g)h = fh + gh, h(f + g) = hf + hg

6. " f, g Î P[x], f × g = g × f

7. " f, g, h Î P[x], (f × g) × h = f × (g × h)

8. " f Î P[x], l × f = f

Проверить каждую аксиому самостоятельно.

§2. Отношение делимости в кольце Р[х] и его свойства.

Определение 1. Многочлен f(х) Î Р[х] делится на многочлен g(x) Î P[x], g(x) ¹ 0, если $ h(x) Î P[x]: f(x)=g(x)×h(x), f(x) - делимое, g(x) -делитель, h(x) - частное.

Задача 1. Выяснить, делится ли многочлен:

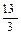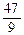f(x) = 3х⁵ - 9х⁴ + х³ – x²- 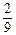x на g(x) = x²- 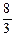х –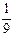

в кольце Q[x].