6. Динамика электропривода
6.1. Силы и моменты, действующие в электроприводе
Состояние привода зависит от действующего вращающего момента двигателя М дв и статического момента сопротивлении М с определяемого нагрузкой производственного механизма. Каждый из моментов может быть движущим и тормозящим. Например, вращение диска пилы или крыльчатки вентилятора: М дв -тормозящий, М с -движущий; опускание краном груза при режиме противовключения двигателя: М дв-тормозящий, М с -движущий; силовой спуск груза – оба момента движущие; электрическое торможение прокатного стана - оба момента тормозящие.
В зависимости от причины, обуславливающей возникновение силы или момента сопротивления, различают активные и реактивные силы и моменты.
Активными (активная нагрузка) называют силы или моменты, которые появляются независимо от движения и создаются посторонними источниками механической энергии. Они всегда направлены в одну сторону, поэтому при изменении направления действия активной нагрузки сохраняется. Примеры: сила притяжение земли, энергия ветра, потока воды, потенциальная энергия грузов, моменты от силы тяжести, растяжения, сжатия и скручивания упругих тел и тому подобное.
Реактивные силы или моменты (реактивная нагрузка) появляется только вследствие движения и направлены против него, то есть они будут всегда тормозящими. При изменении направления вращения двигателя изменяется на противоположное и направление действия реактивной нагрузки. Примеры: механизмы трения в движущих элементах, моменты на рабочих органах металлорежущих станков, механизмы обжатия, резания, подачи жидкости и газа, разрушения неупругих материалов.
Движение электропривода можно рассматривать на каком-либо одном элементе, к которому приведены все внешние силы и моменты, инерционные массы механических звеньев. За такой элемент обычно принимают вал двигателя.
Приведение моментов и сил сопротивления от одной оси вращения к другой выполняется на основании закона сохранения энергии (баланса мощности в механической части привода), например, к валу двигателя
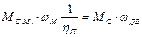 ,
,
откуда
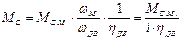 , (6.1)
, (6.1)
где МС.М. – момент сопротивления производственного механизма;
МС - то же момент сопротивления, но приведенный к валу двигателя;
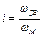 - передаточное число (отношение угловой скорости двигателя w дв к угловой скорости механизма w м);
- передаточное число (отношение угловой скорости двигателя w дв к угловой скорости механизма w м);
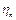 – КПД передачи.
– КПД передачи.
При наличии нескольких передач между двигателем и механизмом с передаточными числами 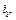
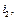 …,
…, 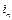 и соответствующими КПД момент сопротивления приведенный к валу электродвигателя
и соответствующими КПД момент сопротивления приведенный к валу электродвигателя
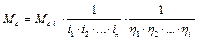 , (6.2)
, (6.2)
Приведение сил сопротивления механизма F с.м к валу электродвигателя выполняется аналогично на том же основании, что и для момента, то есть
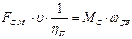 ,
,
откуда
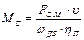 , (6.3)
, (6.3)
где 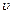 – линейная скорость движения рабочего органа механизма.
– линейная скорость движения рабочего органа механизма.
Приведение моментов инерции к одной оси вращения, например, к валу электродвигателя, основано на том, что суммарный запас кинетической энергии движущих частей привода, отнесенный к одной оси, остается неизменным, то есть
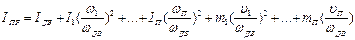 , (6.4)
, (6.4)
где 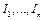 - момент инерции вращающихся частей;
- момент инерции вращающихся частей;
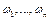 - угловые скорости вращающихся частей;
- угловые скорости вращающихся частей;
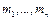 - массы поступательно движущихся частей;
- массы поступательно движущихся частей;
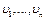 - линейные скорости движущихся частей.
- линейные скорости движущихся частей.
Пример. Необходимо определить приведенные к валу электродвигателя момент сопротивления МС, момент инерции IПР, и мощность на привод РДВ шахтной лебедки (рис. 6.1), если известны: вес груза GГР, вес каната GK, угловая скорость вала электродвигателя 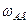 , момент инерции вала электродвигателя IДВ, момент инерции зубчатого колеса 1
, момент инерции вала электродвигателя IДВ, момент инерции зубчатого колеса 1 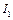 и зубчатого колеса 2 вместе с барабаном
и зубчатого колеса 2 вместе с барабаном 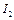 , диаметр барабана ДБ, передаточное отношение
, диаметр барабана ДБ, передаточное отношение 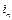 и КПД передачи
и КПД передачи  .
.
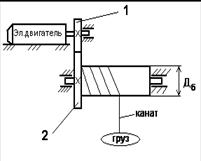
Рис. 6.1. Схема подъема груза с помощью лебедки
Применяя формулы (6.1),(6.4) и формулу, что мощность необходимая на привод 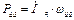 , имеем момент сопротивления
, имеем момент сопротивления 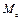 приведенный к моменту двигателя,
приведенный к моменту двигателя,
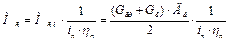 ,
,
момент инерции приведенный к валу двигателя
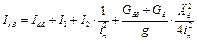 ,
,
мощность необходимую на привод, кВт, при размерностях момента 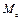 , Нм и угловой скорости двигателя
, Нм и угловой скорости двигателя 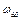 , с–1
, с–1
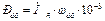
6.2. Уравнение движения электропривода
При изучении движения механической части электропривода возникает необходимость в определении различных механических величин, характеризующих его: пути и угла поворота, скорости и ускорения, моментов и сил, вызывающих движения и других величин, имеющих место в практических вопросах. Для анализа физических процессов в электроприводе в основном используют основное уравнение движения электропривода.
При вращательном движении между моментом, развиваемым двигателем МДВ, и сопротивлением МС нагрузки в системе электродвигатель - производственный механизм существует соотношение, называемое основным уравнением движением электропривода
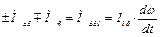 (6.5)
(6.5)
где 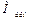 – динамический момент системы;
– динамический момент системы;
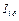 – момент инерции движущихся частей системы, приведенный к валу двигателя;
– момент инерции движущихся частей системы, приведенный к валу двигателя;
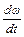 – угловое ускорение системы.
– угловое ускорение системы.
Рис. 6.2. Графическое изображение уравнения движения электропривода.
Знак плюс перед МДВ берется при работе двигателя в двигательном режиме, знак “-” в - тормозном режиме. Знак минус перед МС показывает тормозящее действие статических сопротивлений (подъем груза, усилие резания, сжатие пружины и так далее), знак плюс, когда МС помогает вращению привода (спуск груза, раскручивание пружины и так далее). Знак “+” перед МДИН, а следовательно, и перед 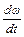 зависит от соотношения величины и знаков МДВ и МС. Когда МДВ>МС, система получает ускорение
зависит от соотношения величины и знаков МДВ и МС. Когда МДВ>МС, система получает ускорение 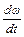 со знаком плюс. При МДВ<МС ускорение системы
со знаком плюс. При МДВ<МС ускорение системы 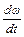 получает отрицательный знак, скорость падает. При МДВ=МС
получает отрицательный знак, скорость падает. При МДВ=МС 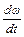 =0 и в данном случае привод работает в установившемся режиме. Динамический момент проявляется только во время переходных режимов, когда изменяется скорость привода. При ускорении привода МДИН направлен против движения, а при торможении он поддерживает движение.
=0 и в данном случае привод работает в установившемся режиме. Динамический момент проявляется только во время переходных режимов, когда изменяется скорость привода. При ускорении привода МДИН направлен против движения, а при торможении он поддерживает движение.
Аналогичные соотношения получаются и для поступательного движения, являющимся простым следствием уравнения вращательного движения
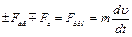 , (6.6)
, (6.6)
где 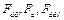 – соответственно усилия, развиваемые двигателем, приведенное статических сопротивлений и динамических сопротивлений;
– соответственно усилия, развиваемые двигателем, приведенное статических сопротивлений и динамических сопротивлений;
m – приведенная масса движущихся частей;
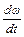 – линейное ускорение движущихся масс.
– линейное ускорение движущихся масс.
6.3. Определение времени переходных процессов в электроприводе
Характер неустановившегося механического движения электропривода, исходя из (6.5), однозначно определяется законом изменения динамического момента, который, являясь функцией моментов двигателя и нагрузки. Рассмотрение неустановившегося движения электропривода позволяет получить зависимости изменения во времени выходных механических координат электропривода – момента 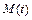 , скорости
, скорости 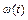 и положение вала двигателя
и положение вала двигателя 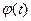 . Обычно законы изменения моментов двигателя и нагрузки должны быть предварительно заданы. В переходных режимах электропровод работает при пуске, торможении и изменении направления вращения, резких колебаниях нагрузки.
. Обычно законы изменения моментов двигателя и нагрузки должны быть предварительно заданы. В переходных режимах электропровод работает при пуске, торможении и изменении направления вращения, резких колебаниях нагрузки.
Определение времени переходных режимов, влияющих на производительность производственных механизмов, основано на интегрировании уравнения движения привода (6.5)
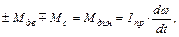
Разделяя переменные, получим
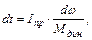 (6.7)
(6.7)
Время, необходимое для изменения скорости привода от 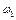 до
до 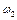
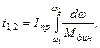 (6.8)
(6.8)
где 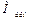 =
= 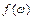 - динамический момент в функции скорости.
- динамический момент в функции скорости.
Для решения этого интеграла необходимо знать зависимость моментов двигателя и механизма от скорости. Функция 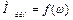 должна иметь аналитическое выражение, которое поддается интегрированию. В простейшем случае, приняв
должна иметь аналитическое выражение, которое поддается интегрированию. В простейшем случае, приняв 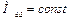 ,
, 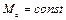 , и
, и 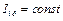 , имеем
, имеем
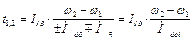 , (6.9)
, (6.9)
Если 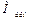 и
и 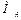 находятся в слишком сложной зависимости от скорости вращения или не поддаются аналитическому выражению, то для определения времени разбега и торможения используются приближенные графические и графоаналитические методы, интегрированные уравнения движения электропривода. Наиболее распространенны графический метод в варианте метода пропорций или конечных пропорций и графоаналитический в варианте метода площадей или последовательных интервалов. Рассматриваем эти методы.
находятся в слишком сложной зависимости от скорости вращения или не поддаются аналитическому выражению, то для определения времени разбега и торможения используются приближенные графические и графоаналитические методы, интегрированные уравнения движения электропривода. Наиболее распространенны графический метод в варианте метода пропорций или конечных пропорций и графоаналитический в варианте метода площадей или последовательных интервалов. Рассматриваем эти методы.
Сущность метода пропорций заключается в замене бесконечно малых приращений конечными приращениями, то есть 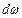 и
и 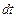 на
на 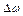 и
и 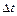 . В основе этого метода лежит уравнение движения привода (6.7)
. В основе этого метода лежит уравнение движения привода (6.7) 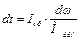 в виде приращений
в виде приращений
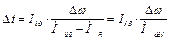 (6.10)
(6.10)
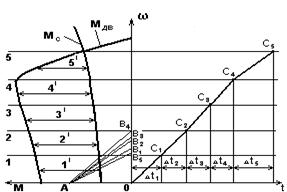
Рис. 6.3. Графический метод получения кривых переходного процесса
Построение осуществляется следующим образом (рис 6.3), показываем ход графического построения кривой t=f( ) и нахождения времени пуска двигателя на примере механических характеристик асинхронного двигателя и вентилятора. В левом квадрате строим характеристики МДВ и МС и графически находим зависимость динамического момента от скорости МДИН (
) и нахождения времени пуска двигателя на примере механических характеристик асинхронного двигателя и вентилятора. В левом квадрате строим характеристики МДВ и МС и графически находим зависимость динамического момента от скорости МДИН ( ). Ось скорости
). Ось скорости  разбиваем на ряд участков (в данном случае на пять участков) до скорости установившегося значения и для каждого участка определяем
разбиваем на ряд участков (в данном случае на пять участков) до скорости установившегося значения и для каждого участка определяем 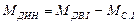 в виде отрезков 1¢, 2¢, 3¢, 4¢, 5¢. На оси абсцисс в масштабе
в виде отрезков 1¢, 2¢, 3¢, 4¢, 5¢. На оси абсцисс в масштабе 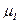 откладываем пропорциональный моменту инерции
откладываем пропорциональный моменту инерции 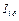 отрезок ОА. Полученные на отдельных участках значения динамического момента откладываем от точки О вверх по оси ординат, в виде отрезков ОВ1=1¢, ОВ2=2¢, ОВ3=3¢, ОВ4=4¢, ОВ5=5¢. Соединяем, отмеченные на оси ординат точки
отрезок ОА. Полученные на отдельных участках значения динамического момента откладываем от точки О вверх по оси ординат, в виде отрезков ОВ1=1¢, ОВ2=2¢, ОВ3=3¢, ОВ4=4¢, ОВ5=5¢. Соединяем, отмеченные на оси ординат точки 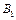 ,
, 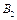 ,
, 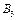 ,
, 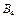 ,
, 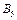 , с точкой А. Проведем линии параллельные оси абсцисс и ограничивающие каждый участок МДИН.I. Затем из начала координат проводим линию
, с точкой А. Проведем линии параллельные оси абсцисс и ограничивающие каждый участок МДИН.I. Затем из начала координат проводим линию 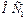 параллельную
параллельную 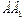 до пересечения с горизонтальной линией, ограничивающую первый участок изменения скорости. Отрезок
до пересечения с горизонтальной линией, ограничивающую первый участок изменения скорости. Отрезок 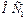 представляет собой график скорости
представляет собой график скорости 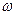 (t) на первом участке моментов. Проведя аналогичные построения для всех последующих участков MДИН.I (
(t) на первом участке моментов. Проведя аналогичные построения для всех последующих участков MДИН.I (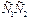 II
II 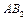 ,
, 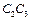 II
II 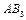 ,
, 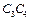 II
II 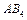 ,
, 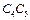 II
II 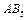 ) строим кривую скорости двигателя и находим искомое время пуска привода. Масштаб времени t определяется из условия, что
) строим кривую скорости двигателя и находим искомое время пуска привода. Масштаб времени t определяется из условия, что 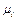 ,
, 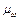 ,
, 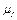 известны, а масштаб времени из условия (6.10), то есть
известны, а масштаб времени из условия (6.10), то есть
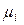 =
= 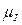
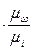 (6.11)
(6.11)
Кроме метода пропорции, для построения кривой угловой скорости используется метод площадей, сводящийся к графоаналитическому интегрированию уравнению движению привода (рис 6.4).
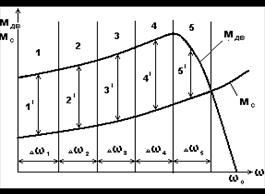
Рис. 6.4. Графоаналитический метод определения времени пуска привода вентилятора
Задаемся механическими характеристиками двигателя МДВ и производственного механизма, совмещают их и определяют момент МДИН.I=MДВ.I-MC.I для каждого участка. Предполагая, что для каждого участка 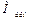 постоянный и равен среднему значению, перепад угловой скорости
постоянный и равен среднему значению, перепад угловой скорости 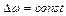 определяется время на i-ом участке будет равно
определяется время на i-ом участке будет равно
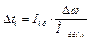 , (6.12)
, (6.12)
Тогда общее время пуска определяется, как
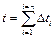 , (6.13)
, (6.13)
где n – число участков (в данном случае n=5).
6.4. Определение оптимального передаточного отношения привода
В ряде практических случаев возникает необходимость в получении минимального времени разгона и торможения производственного механизма с целью улучшения показателей работы системы электропривод-исполнительный орган рабочей машины, в первую очередь производительности машин.
Решим эту задачу при заданных значениях моментов инерции вала двигателя IДВ, производственного механизма IС и момента сопротивления, принимаемого для простейшего случая 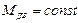 ,
, 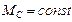 . Пренебрегая потерями в передачах уравнение движения электропривода (6.5) запишется в виде
. Пренебрегая потерями в передачах уравнение движения электропривода (6.5) запишется в виде
i 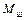 -
- 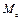 =(
=(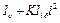 )
) 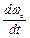 , (6.14)
, (6.14)
где i – передаточное отношение;
К – коэффициент, учитывающий момент инерции передач;
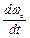 – угловое ускорение исполнительного органа.
– угловое ускорение исполнительного органа.
Очевидно, минимум времени разгона имеет место при небольшом ускорении. Из (6.14)
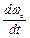 =
= 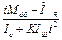 , (6.15)
, (6.15)
Пользуясь правилом определения максимума 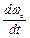 находим оптимальное или наивыгоднейшее передаточное отношение
находим оптимальное или наивыгоднейшее передаточное отношение
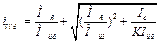 , (6.16)
, (6.16)
Выражение (6.16) справедливо также для обеспечения максимального замедления исполнительного органа.
В том случае, когда момент сопротивления 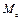 значительно меньше момента двигателя
значительно меньше момента двигателя 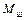 при пуске и торможении
при пуске и торможении
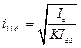 , (6.17)
, (6.17)
Оптимизация передаточного числа может производиться также и по другим показателям, например, по критерию происхождения исполнительным органом максимального пути за заданное время, по критерию минимального времени на прохождение заданного пути.
 2015-02-27
2015-02-27 1374
1374








