Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Легко убедится в том, что для этих функций выполняются сочетательный
x1&(x2&x3)= (x1&x2)&x3,
x1  (x2
(x2  x3)= (x1
x3)= (x1  x2)
x2)  x3,
x3,
переместительный
x1  x2= x1
x2= x1  x2,
x2,
x1& x2= x1&x2,
и распределительный законы. Кроме того, выполняется распределительный закон дизъюнкции относительно конъюнкции.
x1  (x2&x3)= (x1
(x2&x3)= (x1  x2)& (x1
x2)& (x1  x3).
x3).
Проверим справедливость этого закона путем сравнения таблиц для функций, стоящих в левой и правой частях рассматриваемого соотношения.
| x 1 | x 2 | x 3 | x2&x3 | x1  (x2&x3) (x2&x3)
|
| x 1 | x 2 | x 3 | x1  x2 x2
| x1  x3 x3
| (x1  x2)& (x1 x2)& (x1  x3) x3)
|
Совпадение построенных таблиц доказывает наше утверждение.
Рассмотрим теперь ряд простых, но весьма важных соотношений
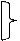 х
х  х=х;
х=х;
х&х=х.
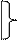
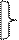
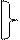 х
х  1=1; х
1=1; х  0=х; х
0=х; х 
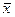 =1;
=1;
х&1=х. х&0=0. х& 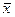 =0.
=0.
И как следствие получаем
х  х
х  …
…  х=х,
х=х,
х&х&…&х=х.
Как обобщение формул получаем следующие формулы, называемые формулами (законами) де Моргана
х1  х2
х2  …
…  хn=
хn= 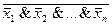 ;
;
х1&х2&…&хn= 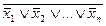 .
.
 2015-02-27
2015-02-27 493
493








