Рассмотрим множество элементарных ФАЛ. Начнем со случая, когда длина слова n=0. По формуле, определяющей число функций логики, вычисляем, что при n=0 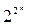 = 2.
= 2.
f1=0; f2=1.
Эти две функции совпадают с константами.
В случае n=1 мы имеем две функции, существенно зависящие от аргумента x, эти две функции определяются таблицей
| x1 | f 3 | f 4 |
Эти две функции также относят к элементарным, и они записываются следующим образом
f 3=x; f 4= 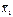 ( читается «не x» ).
( читается «не x» ).
Функцию f 4 называют функцией отрицания.
В случае n=2 имеем десять различных функций, существенно зависящих от аргументов x1 и x2.
| x1 Ú x2 | x1 & x2 | x1 ~ x2 | x1 ® x2 | x1 ¯ x2 | x1 / x2 | x1 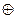 x2 x2 | ||
| x 1 | x 2 | f 5 | f 6 | f 7 | f 8 | f 9 | f 10 | f 11 |
Функция f5(x1,x2) = x1 Ú x2 (дизъюнкция).
Функция f6(x1,x2) = x1 & x2 (конъюнкция).
Вместо символов & часто применяют символ умножения «•» или вообще опускают также, как и в обычной алгебре.
Функция f7 носит название функции эквивалентности или функции равнозначности
f7(x1,x2) = x1 ~ x2
и f7(x1,x2) = x1 º x2.
Функция f8 носит название импликации x1 в x2. Она обозначается f8(x1,x2) = x1 ® x2.
Функция f9 носит название функции Вебба (или ее называют еще стрелкой Пирса) и обозначается
f 9(x1,x2) = x1 v x2.
Функция f9 называется функцией (штрихом) Шеффера и обозначается следующим образом f 10(x1,x2) = x1 ¯ x2.
Функция f 11 обычно называется функцией сложения по модулю 2.
f 11(x1,x2) = x1 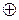 x2.
x2.
Рассмотрение одиннадцати функций позволяют строить новые функции двумя основными способами:
1. путем перенумерации аргументов;
2. путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f 1, f 2, f 3, …, f k путем применения этих правил будем называть суперпозицией функции f 1, f 2, f 3, …, f k.
Имея, например, элементарные функции отрицания, дизъюнкции, эквивалентности и импликации, можно составить следующие новые функции ФАЛ.
Используя таблицы, определяющие элементарные функции, можно задать любую функцию ФАЛ, являющуюся суперпозицией этих функций.
Пример. Пусть требуется представить в виде таблицы следующую функцию
f (x1,x2,x3)={[( ~ x2) Ú (x1 ¯ x2)] (x1
~ x2) Ú (x1 ¯ x2)] (x1 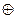 x2)} ® x3.
x2)} ® x3.
Будем строить ФАЛ последовательно.
| x1 | x 2 | x 3 | 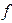  |  ~ x2 ~ x2 | x1 ¯ x2 | [ ] | x1 Ú x2 | { } | f (x1,x2,x3) |
ВЫРАЖЕНИЕ ОДНИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
1. Функция f 8(x1,x2) = x1 ® x2 (импликация x1 в x2) может быть записана посредством функций дизъюнкции и отрицания
x1 > x2=  Ú x 2.
Ú x 2.
Доказательство осуществляется посредством таблиц истинности.
| x 1 | x 2 | x1 ® x2 |
| x1 | x 2 |   |  Ú x 2 Ú x 2 |
2. Функцию эквивалентности f7(x1,x2) = x1 ~ x2 = x1 º x2 выразим посредством других функций x1 ~ x2= ( Ú x2)&(x 1 Ú
Ú x2)&(x 1 Ú 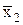 )
)
| x 1 | x 2 | x1 ~ x2 | ||||
| x 1 | x 2 |  | 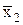 |  Ú x 2 Ú x 2 | x1 Ú 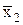 | ( Ú x2)&(x 1 Ú Ú x2)&(x 1 Ú 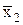 ) ) |
3. f 11(x1,x2) = x1 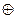 x2=
x2= 
| x 1 | x 2 | x1 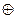 x2 x2 | x1 ~ x2 | 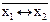 |
или
f (x1,x2) = x1 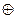 x2=(
x2=( & x2)
& x2)  (x1&
(x1& 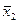 )
)
| x 1 | x 2 | x1 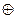 x2 x2 |  | ( &x2) &x2) | 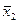 | (x1& 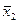 ) ) | ( &x2) &x2)  (x1& (x1& 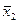 ) ) |
4. 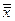 = x
= x
| x |  | 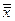 |
5. x1& x2= 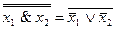
| x 1 | x 2 | x1& x2 |
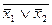
| x 1 | x 2 |  | 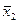 |   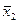 | 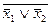 |
6. x1  x2=
x2= 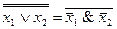
| x 1 | x 2 | x1  x2 x2 |
| x 1 | x 2 |  | 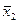 |  & & 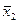 | 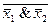 |
7. x1 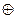 x2=
x2= 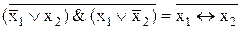
| x 1 | x 2 | x1 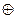 x2 x2 |
| x 1 | x 2 |  | 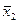 |   x2 x2 | x1  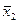 | 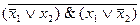 |
 2015-02-27
2015-02-27 1633
1633
