2015-02-27
456
ФАЛ называется функция, дающая однозначное отображение Х в Y.
1. Число различных ФАЛ, зависящих от n аргументов, конечно и равно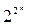 
.
| x1, x2, …, xn-1, xn | f (x1, x2, …, xn-1, xn) |
| 0 0 … 0 0 | α1 |
| 0 0 … 0 1 | α2 |
| … … … … … | … … …… … … … |
| 1 1 … 1 0 |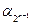 
|
| 1 1 … 1 1 |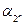 
|
Если наборам значений аргументов ФАЛ сопоставляет точки n- мерного пространства, то множество 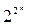наборов определяет множество вершин n- мерного единичного куба. Таким образом, областью определения ФАЛ, зависящей от n аргументов, является множество вершин такого куба.
Пример.
ФАЛ f(x1, x2, x3) может быть задана геометрически. f(101, 110, 010, 011)=1
|
Значения ФАЛ могут быть заданы не на всех возможных наборах аргументов. На некоторых значения функции могут быть не определены. Такие функции называют не полностью определенными.
2. Если две ФАЛ f1(x1, x2, …, xn-1, xn) и f2(x1, x2, …, xn-1, xn) принимают на всех возможных наборах значений аргументов одинаковые значения, то функции f1 и f2 называются равными.
3. ФАЛ f(x1, x2, …, xi, xi+1, …, xn-1, xn) существенно зависит от аргумента xi, если имеет место соотношение
f(x1, x2, …, xi-1,0, xi+1, …, xn-1, xn)¹ f(x1, x2, …, xi-1,1, xi+1, …, xn-1, xn)
в противном случае говорят, что от xi функция зависит не существенно и xi является ее фиктивным аргументом. ФАЛ не изменяется, если к ее аргументам дописать любое число фиктивных аргументов или зачеркнуть те аргументы, которые являются фиктивными.
Как найти несущественные аргументы? Для этого, если ФАЛ задана таблично, поступают следующим образом.
Разбивают множество наборов аргументов функции на два подмножества:
- подмножество, на котором заданная функция принимает значение 1;
- подмножество, на котором заданная функция принимает 0.
Для проверки фиктивности аргумента xi вычеркивают столбец, ему соответствующий, и проверяют, не появились ли в обоих подмножествах одинаковые наборы. Если таких наборов не появилось, то xi является фиктивным аргументом.
Пример:
Таблица
| x1 x2 x3 x4 | f (x1, x2, x3, x4) |
| 0 0 0 0 | |
| 0 0 0 1 | |
| 0 0 1 0 | |
| 0 0 1 1 | |
| 0 1 0 0 | |
| 0 1 0 1 | |
| 0 1 1 0 | |
| 0 1 1 1 | |
| 1 0 0 0 | |
| 1 0 0 1 | |
| 1 0 1 0 | |
| 1 0 1 1 | |
| 1 1 0 0 | |
| 1 1 0 1 | |
| 1 1 1 0 | |
| 1 1 1 1 |
Произведем разбиение набора аргументов:
x1 x2 x3 x4
0 0 0 0
0 0 0 1 x1 x2 x3 x4
0 0 1 0 0 1 0 0
0 0 1 1 наборы х 0 1 0 1
0 1 1 0 на которых 1 1 0 0 f(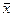
)= 1
0 1 1 1 f(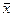)= 0 1 1 0 1
1 0 0 0 1 1 1 0
1 0 0 1 1 1 1 1
1 0 1 1
Вычеркнем в наборах четвертый столбец. Оставшиеся наборы таковы, что ни один из них не входит одновременно в оба подмножества. Это свидетельствует о фиктивности аргумента x4.
