Отношение равносильности и эквивалентность

Докажем, что если формулы j₁ и j₂ равносильны, то формула j₁«j₂ тождественно истинна, то есть если j₁ºj₂, то |‑j₁«j₂ и если |‑j₁«j₂, то j₁ºj₂.

Доказательство. Действительно, если j₁ºj₂, то формулы j₁ и j₂ принимают обе значение И или обе значение Л при любом наборе значений входящих в них переменных, а в этом случае формула j₁«j₂, согласно определению эквивалентности, принимает только значение И, то есть |‑j₁«j₂. Обратно, если ‑j₁«j₂, то j₁ и j₂ принимают при любом наборе значений входящих в них переменных обе значение И или обе значение Л, то есть j₁ºj₂.

Таким образом, исходя из доказанного предложения, каждая из перечисленных в таблице равносильностей порождает тождественно истинную формулу (достаточно заменить знак равносильности = или º знаком эквивалентности «).

Наоборот, если j₁¹j₂, то для некоторого набора x ₁,…, x _n значений переменных одно высказывание будет иметь значение И, другое – Л. Тогда j₁(x ₁,…, x _n) «j₂(x ₁,…, x _n) будет ложным высказыванием, а следовательно, формула j₁(x ₁,…, x _n) «j₂(x ₁,…, x _n) не будет тождественно истинной.

Тем самым задача об установлении равносильности двух формул сводится к установлению тождественной истинности формул частного вида.

Наряду с отношением равносильности между формулами логики высказываний рассматриваются некоторые другие отношения, представляющие большой интерес для логики и ее приложений. Среди них наиважнейшим является отношение логического следования.

Пусть j₁(x ₁,…, x _n)ºj₁ и j₂(x ₁,…, x _n)ºj₂ – две формулы логики высказываний от переменных x ₁,…, x _n. Будем говорить, что формула j₂(x ₁,…, x _n) является логическим следствием формулы j₁(x ₁,…, x _n), если j₂ принимает значение И для всех наборов значений переменных, для которых j₁ истинна. Это означает также, что если представить обе формулы их таблицами истинности, то множество наборов, для которых j₁ истинна содержится в множестве наборов, для которых истинна формула j₂.

Например, согласно этому определению j₂=(x Ú z) является логическим следствием j₁=((x Ú y)& z). Это видно их соответствующих таблиц истинности.

Определение. Формула j₂(x ₁,…, x _n) является логическим следствием формулы j₁(x ₁,…, x _n) тогда и только тогда, когда тождественно истинна формула

j₁(x ₁,…, x _n)®j₂(x ₁,…, x _n).

Из сказанного видно, что формулы j₁ и j₂ равносильны тогда и только тогда, когда каждая из них является логическим следствием другой. Из определения также следует, что всякая формула является логическим следствием тождественно ложной формулы. Действительно, так как в этом случае формула j₁ никогда не принимает значение И, то множество наборов, для которых j₁ истинно, пусто и содержится, следовательно, в множестве наборов истинности для любой формулы j₂.

Отметим, что введенные отношения (тождества и следования) относятся не к единичным высказываниям, как это имело место для понятия импликации, а к целым множествам высказываний, описываемых формулами j₁(x ₁,…, x _n) и j₂(x ₁,…, x _n).

Формулу j₁(x ₁,…, x _n) можно рассматривать как условие, которое может быть выполнимо или нет в зависимости от истинности j₁.

Перечень тождественно истинных формул

1. (p Þ q)(r Þ q)Û(p Ú r Þ q);

2. pq Þ p;

3. (p Þ q)(p Þ r)Û(p Þ qr);

4. (p Þ q) p Þ q;

5. ;

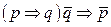6. 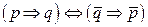‑ закон контрапозиции;

7. 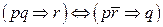? ‑ закон расширенной контрапозиции;

8. p Þ(q Þ r)Û pq Þ r;

9. ;

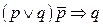10. ;

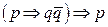11. (p Þ q)(q Þ r)Û(p Þ r) –.закон силлогизма.

Подстановка

Разумеется, этот перечень не исчерпывает тождественно истинные формулы, находящие применение в исчислении высказываний. Вместе с тем каждая из перечисленных тождественно истинных формул порождает новые ТИФ в результате подстановки вместо какой-нибудь входящей в нее переменной произвольной формулы.

Действительно, если |‑j(…, р,…) содержит переменную р, то, подставив вместо переменной р всюду, где она входит в j, произвольную формулу y, в результате получим формулу j(…, y,…), которая принимает те же значения, что и исходная формула j(…, р,…), так как y принимает те же значения (И, Л), что и р.

Конечно, можно применять подстановку к нескольким или даже ко всем переменным, входящим в ТИФ.

Например, тождественно истинной формулой является

|‑(j₁Þj₂)(j₂Þj₃)Û(j₁Þj₃), так как эта формула получается из (11) подстановкой вместо p формулы j₁, вместо q формулы j₂ и вместо r формулы j₃.