2015-02-27
266
Обратимся к рис.4.7. Дисперсия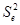 
характеризует ошибку эксперимента. Её можно получить путем возведения в квадрат разности 
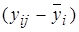с последующим суммированием по всем экспериментальным точкам:
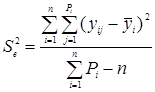(4.22)
Знаменатель дисперсии равен разности между общим количеством экспериментальных точек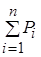 
и числом наложенных связей n, т.к. каждая выборка дает одну связь.
Дисперсия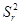 
характеризует неточность подгонки модели, её неадекватность. Поэтому её можно получить из разности 
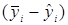, которая после возведения в квадрат и суммирования представляет собой сумму квадратов отклонений относительно эмпирической линии регрессии:
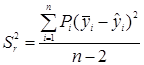(4.23)
Здесь число степеней свободы равно (n-2). Две связи вызваны двумя ограничениями, связанными с определением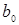 
и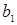 
.
Если математическое ожидание дисперсии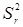 
равно дисперсии выходной величины h:
,
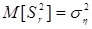то полученная эмпирическая модель будет корректной.
