Уравнение линии на плоскости

Линия и прямая на плоскости. Прямая и плоскость в пространстве

План:

1. Уравнение линии на плоскости.

2. Каноническое и параметрическое уравнение прямой.

3.Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

4.

Уравнение линии на плоскости

Прямую можно определить только двумя способами:

· дана одна точка и угловой коэффициент;

· даны две точки.

Всякое уравнение относительно x,y вида

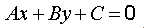(1)

где 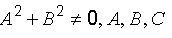– постоянные коэффициенты, называется общим уравнением прямой и однозначно определяет на плоскости некоторую прямую. Bектор 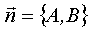перпендикулярен прямой, т. е. будет её нормальным вектором. Рассмотрим частные случаи.

1) 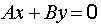, прямая проходит через начало координат, когда ;

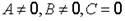2) 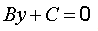, или 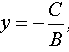когда A=0; горизонтальная прямая (параллельна оси Ox);

3) 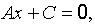или 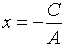при B=0 – вертикальная прямая (параллельна оси Oy).

Уравнению с переменными х и у соответствует на плоскости некоторая линия, координаты точек которой удовлетворяют данному уравнению. Построение графиков функций можно рассматривать как примеры нахождения линий, соответствующих данным уравнениям.

Уравнением данной линии (в выбранной на плоскости системе координат) называется такое уравнение с переменными х и у, которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.