Префиксные (древовидные) коды

Рассмотренная в предыдущем пункте схема кодирования предполагала преобразование каждого блока входящих информационных символов 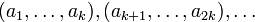в кодовые слова одинаковой длины 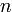. Такое правило позволяет легко отделить кодовые слове по прохождении сообщением канала связи. Можно ли осуществить кодирование с переменной длиной кода? Следующий пример указывает на одну серьезную проблему, которая может встретиться при таком способе.

П

Пример. Пусть кодирование производится по правилу:

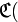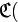а)=1, в)=01, 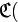о)=010, 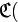с)=001.

Кодирование сообщения

а о в а о о с

дает кодовую последовательность

.

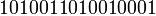
Попытаемся ее декодировать. Первая цифра однозначно декодируется в а (поскольку ни одно другое кодовое слово не начинается с 1). Следующая цифра в коде — 0, она может быть начальной цифрой кодового слова для любой из трех букв в, о или с. Следующая за ней цифра — 1. Пара (0,1) может быть кодовым словом для буквы в, либо же быть начальным отрезком (блоком) для кодового слова, соответствующего букве о. Берем следующую цифру кода — 0. И здесь декодер сталкивается с неоднозначностью толкования: либо кодовую последовательность следует разбить как 1 | 010 |, либо же — как 1 | 01 | 001 — и оба варианта имеют право на существование! ♦

Код называется префиксным1) если ни одно его кодовое слово не совпадает с начальным отрезком какого-то другого кодового слова.

Пример. Код 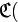(а)=1, 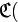в)=01, 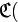о)=010, 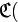с)=001. является префиксным. Префиксность кода позволяет декодеру разбить поток закодированного сообщения на отдельные кодовые слова единственно возможным способом, так что сообщение

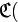разбивается на блоки 1 | 000 | 01 | 1 | 000 | 000 |.001 ♦

Очевидно, что для любого набора двоичных символов , не входящего в состав префиксного кода 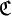, возможно два варианта:

1. в 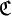нет кодового слова вида 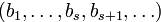, т.е. такого, у которого начальный отрезок совпадал бы с данным;

2. в 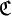существует кодовое слово с указанным свойством.

В последнем случае наборы 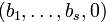и 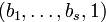будут либо кодовыми словами либо начальными отрезками кодовых слов кода .

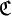Префиксный код называется примитивным, если его невозможно сократить, т.е. если при вычеркивании любого знака хотя бы в одном кодовом слове код перестает быть префиксным.

Пример. Закодируем буквы русского алфавита по таблице.

а	б	в	г	д	е	ж	з	и	к

Легко проверить, что этот код — примитивный префиксный. Его можно изобразить в виде особого графа — дерева, у которого из корня и любой вершины, кроме свободных, выходят по две ветви. Если мы условимся всегда сопоставлять каждой верхней ветви0, а каждой нижней ветви — 1, то каждой свободной вершине дерева будет однозначно соответствовать набор нулей и единиц, показывающий, в каком порядке нужно сворачивать вверх или вни 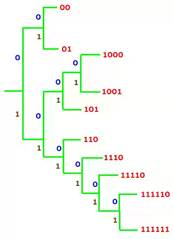з, добираясь до этой вершины из корня дерева.

Граф кода называется его деревом, отсюда идет другое название префиксных кодов — древовидные.

Теорема. Пусть в примитивном префиксном коде число кодовых слов, состоящих из k двоичных знаков, обозначается Nк, а r означает число знаков в самом длинном кодовом слове. Тогда справедливо равенство

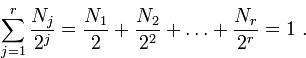
Для последнего рассмотренного примера имеем

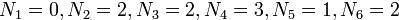и

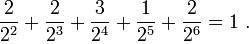
Сколько существует различных префиксных кодов, состоящих из 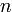кодовых слов? Этот вопрос можно переформулировать в вопрос о количестве деревьев с 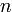«листьями» (их принято называть висячими вершинами), построенных по указанному в примере правилу. В таком виде (и в различных ее обобщениях и приложениях) задача впервые была поставлена в XIX веке Артуром Кэли [3].

Теорема. Количество различных префиксных кодов, состоящих из 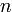кодовых слов, равно

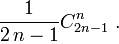
Здесь 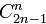— биномиальный коэффициент.

Пример. Для это число равно.

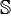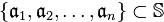Задача. Пусть означает бинарную операцию на множестве и ,.. Сколько различных значений (в зависимости от расстановок скобок) может принимать выражение ?

Оказывается, последовательность выполнения операций удобно изобразить схематично в виде дерева. Так, на рисунке

указаны всех возможных вариантов расстановки скобок при вычислении выражения . Поставил исходную задачу и «деревообработал» ее Кэли в XIX веке.

Итак, каждое дерево имеет ровно один корень и «листьев», которые принято называть висячими вершинами. Корни и «листья» связаны собственно деревом, вид которого ограничивается единственным условием: из каждой точки ветвления (они также называются вершинами, только невисячими) должно выходить ровно по две ветки (таким образом количество таких точек ветвления равно 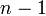). Итак, поставленная выше задача переформулируется в ей эквивалентную —

Теорема [Р.Болл].1) Максимальное количество значений выражения в зависимости от расстановок в нем скобок равно

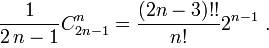
Здесь 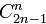— биномиальный коэффициент, а 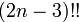означает произведение всех нечетных чисел от 1 до .

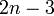Пример. n 3 4 5 10

число Болла 2 5 14 4862

Укажем еще одно применение деревьев — уже относящееся к XX веку. Пронумеруем ветви дерева: каждой правой ветви, идущей из невисячей вершины, поставим в соответствие 1, каждой левой — 0. В результате, путь, ведущий из корня до каждой висячей вершины, оказывается закодированным.

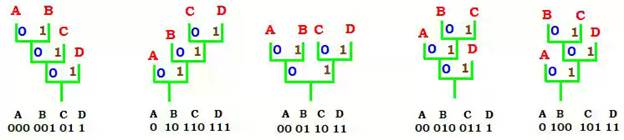
Расставив в вершинах буквы (символы), которые нужно закодировать, получим их выражения в виде двоичных последовательностей — кодовых слов. Разным деревьям соответствуют разные коды. Все они обладают свойством, которое называется префиксностью