Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем.
Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий.
Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Пример кодового дерева
Исходные символы:
A (частота встречаемости 50)
B (частота встречаемости 39)
C (частота встречаемости 18)
D (частота встречаемости 49)
E (частота встречаемости 35)
F (частота встречаемости 24)
Кодовое дерево
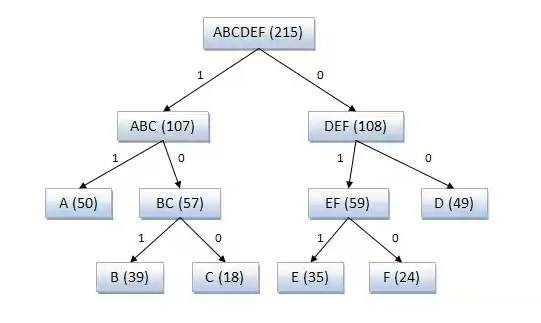
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона-Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Пример 1. Закодируем буквы алфавита в коде Шеннона-Фано.
Пусть имеется случайная величина X (x1, x2, x3, x4, x5, x6, x7, x8), имеющая восемь состояний с распределением вероятностей 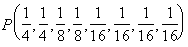
Для кодирования алфавита из восьми букв без учета вероятностей равномерным двоичным кодом нам понадобятся три символа:
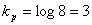 Это 000, 001, 010, 011, 100, 101, 110, 111
Это 000, 001, 010, 011, 100, 101, 110, 111
Чтобы ответить, хорош этот код или нет, необходимо сравнить его с оптимальным значением, то есть определить энтропию
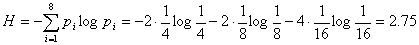
Определив избыточность L по формуле L=1-H/H0=1-2,75/3=0,084, видим, что возможно сокращение длины кода на 8,4%.
Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д. (см.табл.4.1)
Таблица 4.1.
| X | P | Коды | ||||
| x1 | 1/4 | ------- | ------- | |||
| x2 | 1/4 | ------- | ------- | |||
| x3, | 1/8 | ------- | ||||
| x4 | 1/8 | ------- | ||||
| x5 | 1/16 | |||||
| x6 | 1/16 | |||||
| x7 | 1/16 | |||||
| x8 | 1/16 |
Средняя длина полученного кода будет равна
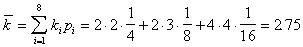
Итак, мы получили оптимальный код. Длина этого кода совпала с энтропией. Данный код оказался удачным, так как величины вероятностей точно делились на равновероятные группы.
Пример 2.
Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит включен и пробел, частота которого составляет 0,145. Метод кодирования представлен в таблице
| Буква | Рi | Код | ||||
| ? | 0.145 | - | ||||
| о | 0.095 | - | ||||
| е | 0.074 | |||||
| а | 0.064 | |||||
| и | 0.064 | |||||
| н | 0.056 | |||||
| т | 0.056 | … | … | - | ||
| с | 0.047 | … | … | |||
| ... | … | |||||
| ф | 0.03 |
Средняя длина данного кода будет равна, 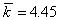 бит/букву;
бит/букву;
Энтропия H=4.42 бит/буква. Эффективность полученного кода можно определить как отношение энтропии к средней длине кода. Она равна 0,994. При значении равном единице код является оптимальным. Если бы мы кодировали кодом равномерной длины 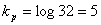 , то эффективность была бы значительно ниже.
, то эффективность была бы значительно ниже. 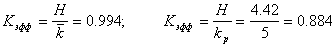
 2015-02-27
2015-02-27 27283
27283








