2.1. Запустите на выполнение среду программирования Microsoft Excel. По умолчанию создается новый документ. Сохраните документ на рабочий диск под уникальным именем:
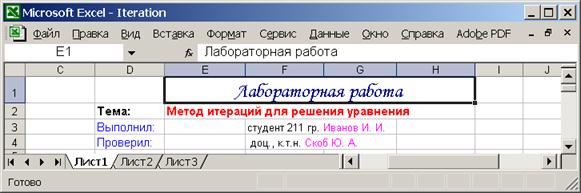
2.2. Введите необходимую текстовую информацию для идентификации работы:
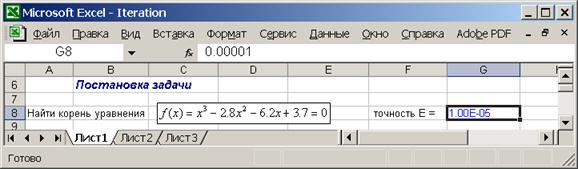
2.3. Внесите информацию о постановке задачи:
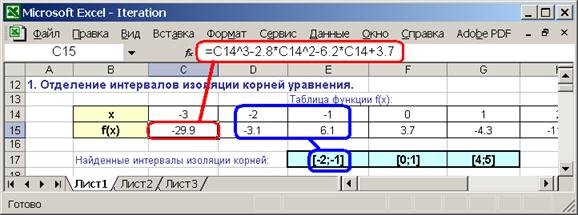
2.4. Для определения интервалов изоляции корней уравнения построим таблицу значений функции 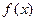 . Выделите интервалы аргумента, на которых функция меняет знак – это интервалы изоляции корней уравнения. Выберите один из интервалов для нахождения корня методом итерации:
. Выделите интервалы аргумента, на которых функция меняет знак – это интервалы изоляции корней уравнения. Выберите один из интервалов для нахождения корня методом итерации:
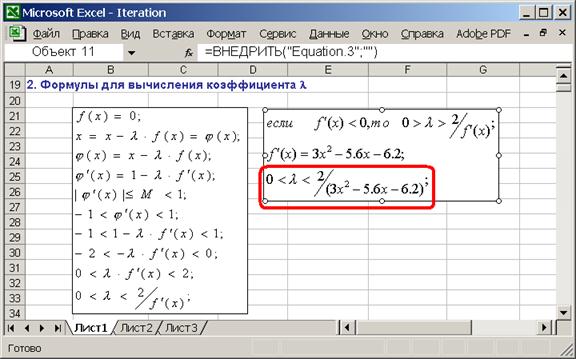
2.5. Введите справочную информацию о методе:
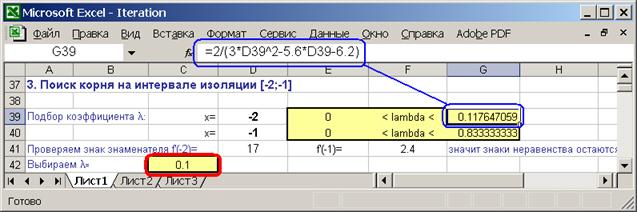
2.6. Подберите значение l, которое обеспечит устойчивое схождение итерационного процесса к корню:
2.7. Постройте заголовок таблицы нахождения корня. Внесите начальное значение номера итерации и формулу для остальных номеров:
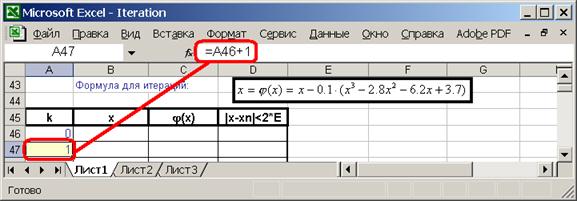
2.8. Внесите начальное значение x – середину интервала изоляции:
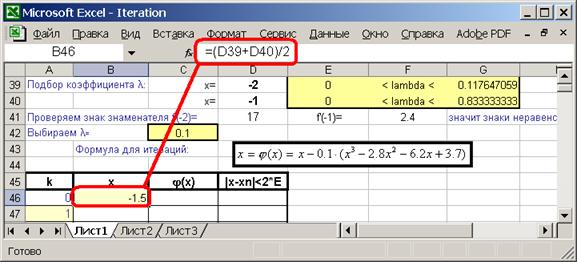
2.9. Вычислите правую часть итерационного уравнения 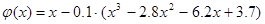 :
:
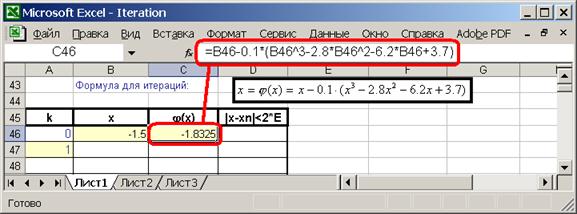
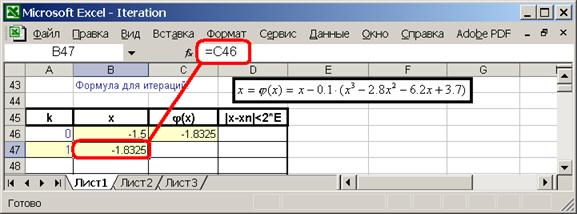
2.10. Введите формулу нового значения 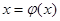 :
:
2.11. Введите формулу условия прекращения итераций 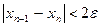 :
:
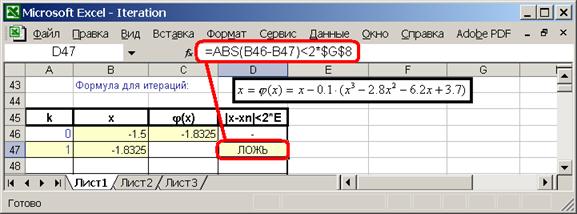
2.12. Распространите формулы на нижнюю часть таблицы:
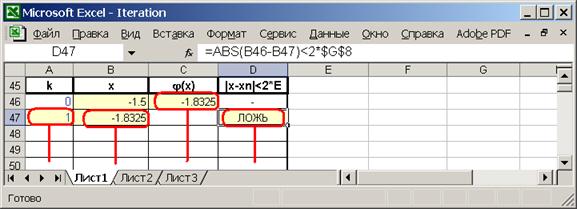
2.13. Расчеты можно проводить до строки, в которой условие в столбце D выполнится. Выведите окончательное значение корня уравнения:
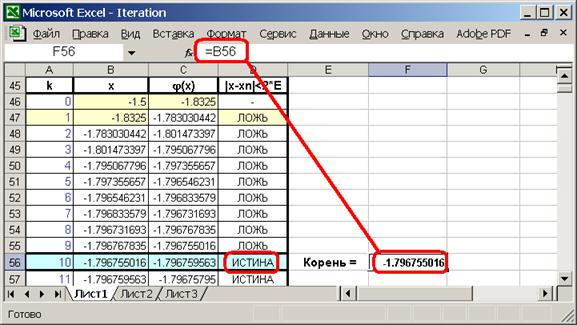
2.14. Сравните результаты, полученные в других средах программирования.
3. Расчет в среде программирования Fortran.
3.1. Запустите на выполнение среду программирования Developer Studio.
3.2. Создайте проект Lab16_V1 приложения Windows, выполняющего задание (команда меню File | New…).
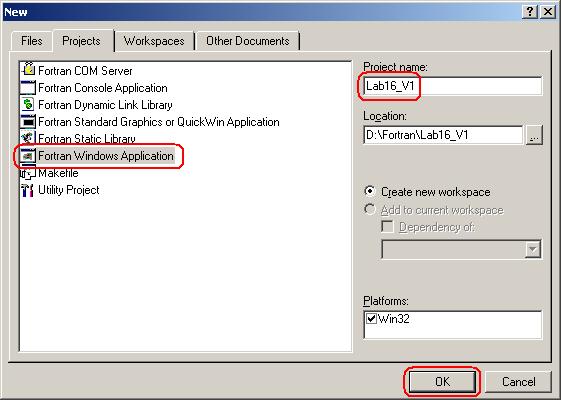
3.3. В открывшемся следующем окне мастера выберите переключатель A simple Dialog based Application. Подтвердите выбранные опции, нажав Finish.
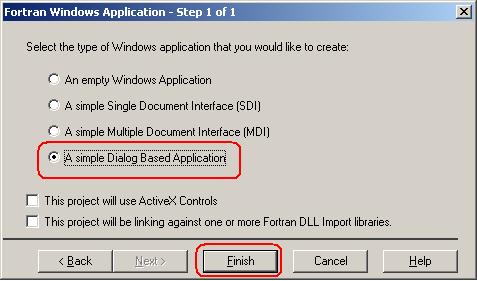
3.4. Ознакомьтесь с окончательной информацией о создаваемом проекте и нажмите на кнопку OK.
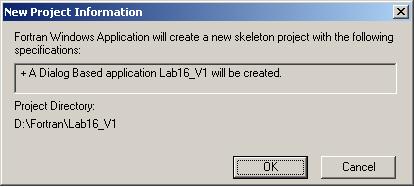
3.5. Мастер сгенерирует проект диалогового приложения, которое можно откомпилировать и запустить на выполнение. Создан ряд файлов, название которых основано на имени проекта.
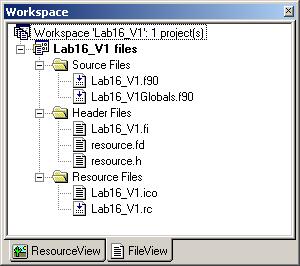
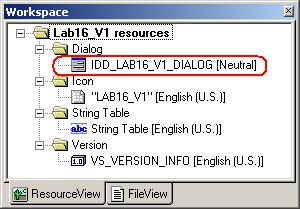
3.6. Кроме того есть папка ресурсов проекта ResourceView, перейдя на которую можно отредактировать графические и строковые ресурсы проекта.
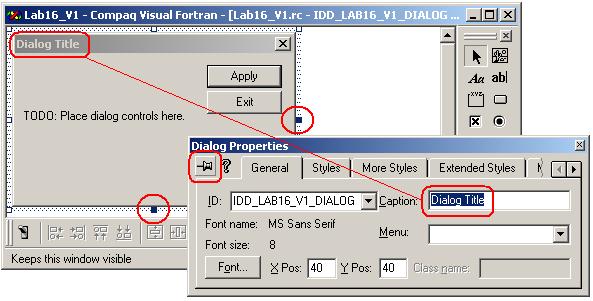
3.7. Двойной щелчок левой кнопки мыши по идентификатору диалоговой панели IDD_LAB16_V1_DIALOGприводит к открытию редактора диалога. Шаблон диалоговой панели по умолчанию содержит две командные кнопки Apply и Exit, метку с надписью посередине, строку заголовка с именем «Dialog Title» и с кнопкой завершения работы программы  . Каждый элемент на панели (как и саму панель) можно выделить левой кнопкой мыши. При этом вокруг выделенного элемента возникает рамка с габаритными маркерами, «потянув» за которые левой кнопкой мыши можно изменить габариты текущего (выделенного) элемента. Кроме того, для текущего элемента можно с помощью контекстного меню (вызывается правой кнопкой мыши над элементом) вызвать панель свойств Properties и посмотреть (или изменить) свойства элемента. Чтобы панель свойств не закрылась, ее можно «закрепить» на экране с помощью кнопки
. Каждый элемент на панели (как и саму панель) можно выделить левой кнопкой мыши. При этом вокруг выделенного элемента возникает рамка с габаритными маркерами, «потянув» за которые левой кнопкой мыши можно изменить габариты текущего (выделенного) элемента. Кроме того, для текущего элемента можно с помощью контекстного меню (вызывается правой кнопкой мыши над элементом) вызвать панель свойств Properties и посмотреть (или изменить) свойства элемента. Чтобы панель свойств не закрылась, ее можно «закрепить» на экране с помощью кнопки  .
.
3.8. Представим возможный финальный вид диалоговой панели, которая принимает от пользователя исходные данные и выводит результаты.
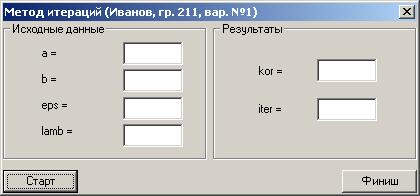
3.9. С помощью палитры компонентов Dialog добавьте на форму компоненты в соответствии с таблицей:
| Компонент | Инструмент | Назначение | Идентификатор |
| Group Box 1 | 
| Контейнер ввода исходных данных | |
| Group Box 2 | 
| Контейнер вывода результатов расчета | |
| Edit Box 1 | 
| Окно ввода левой границы интервала a | IDC_EDIT_A |
| Edit Box 2 | 
| Окно ввода правой границы интервала b | IDC_EDIT_B |
| Edit Box 3 | 
| Окно ввода точности расчета e | IDC_EDIT_EPS |
| Edit Box 4 | 
| Окно ввода коэффициента l | IDC_EDIT_LAMB |
| Edit Box 5 | 
| Окно вывода корня уравнения 
| IDC_EDIT_KOR |
| Edit Box 6 | 
| Окно вывода количества итераций | IDC_EDIT_ITER |
| Static Text 1- Static Text 6 | 
| Соответствующие поясняющие метки |
3.10. В результате форма может выглядеть так:
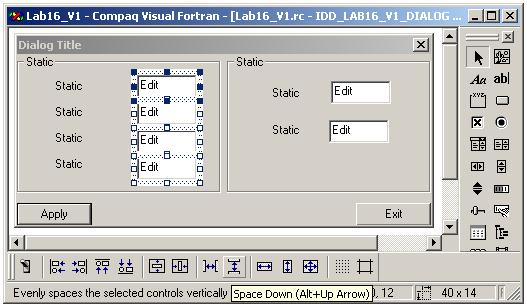
3.11. Измените заголовки меток, формы и контейнеров группировки, а идентификаторы окон редактирования (см. таблицу п. 3.9), используя панель свойств Properties. Идентификаторы командных кнопок, меток и самой панели оставьте без изменений.
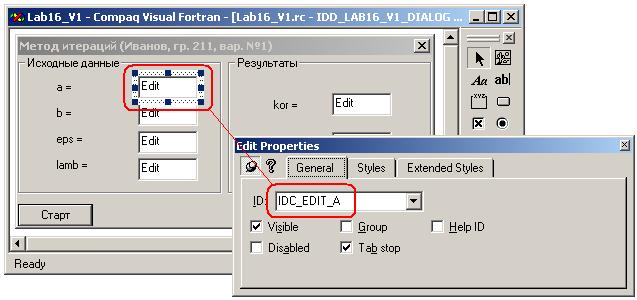
3.12. Протестируйте внешний вид диалоговой панели с помощью инструмента  на палитре выравнивания.
на палитре выравнивания.

3.13. Внесите изменения в исходный текст программы в соответствии с заданием варианта.
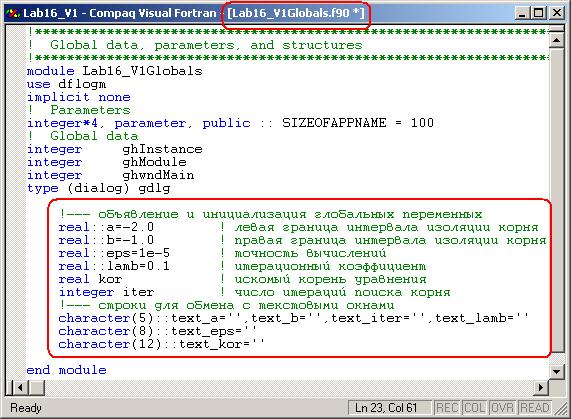
· Введите в модуль Lab16_V1Globals (файл Lab16_V1Globals.f90 проекта) в качестве глобальных данных соответствующие переменные для исходных данных и результатов расчета. Связь между этими переменными и соответствующими окнами редактирования на диалоговой панели приложения будет осуществляться через одноименные строковые переменные с приставкой text_.
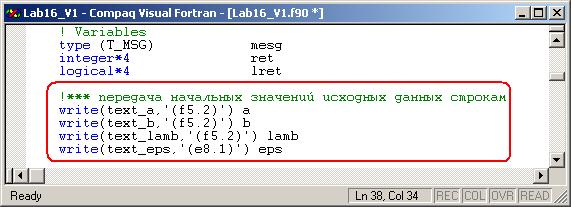
· Отредактируйте файл Lab16_V1.f90. В теле главной функции приложения WinMain сразу за разделом объявлений передайте начальные данные от глобальных переменных исходных данных их соответствующим строкам.
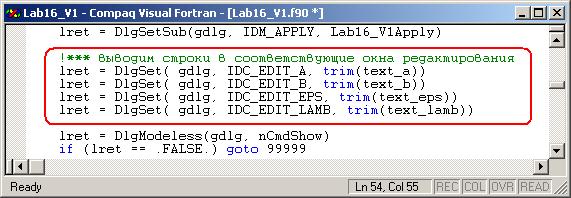
· Перед оператором запуска диалоговой панели в немодальном режиме передайте начальные значения исходных данных в окна редактирования с соответствующими идентификаторами.
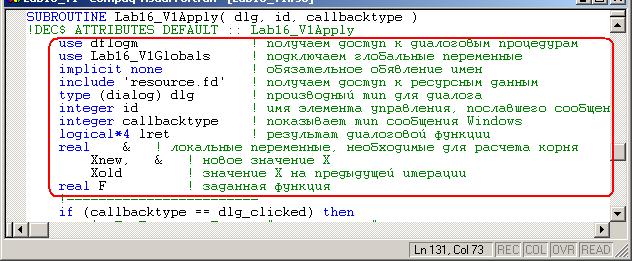
· Отредактируйте подпрограмму Lab16_V1Apply – обработчик сообщений кнопки «Финиш» (бывшая кнопка «Apply»). В начале этой процедуры объявите необходимые переменные. Часть объявлений уже создана мастером.
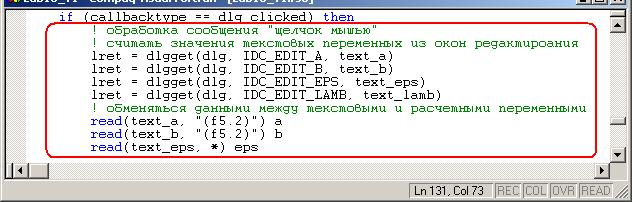
· Далее в операторе обработки нажатия левой кнопки мыши (сообщение dlg_clicked) вместо комментария «TO DO» считайте с помощью функции dlgget из окон редактирования исходные данные в текстовые переменные и обменяйте данные между ними и расчетными переменными, применив оператор read.
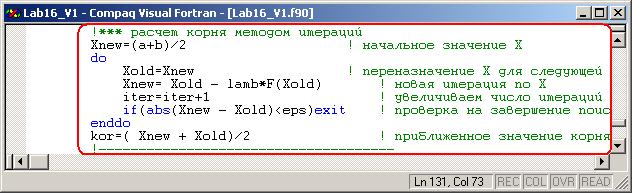
· Теперь вычислите приближенное значение корня уравнения методом половинного деления с заданной точностью.
· В завершение обработки сообщения выведите значения результатов на диалоговую панель посредством буферных текстовых переменных.
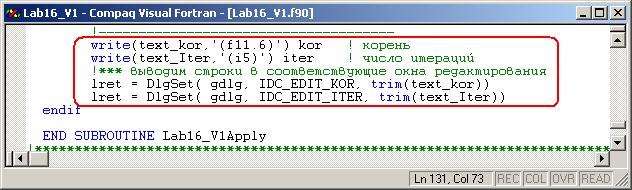
· После процедуры-обработчика сообщений поместите процедуру, вычисляющую заданную функцию.

3.14. Компилируйте проект и запустите на выполнение с помощью команды меню Build | Execute (Ctrl+F5). Появится диалоговое окно приложения.
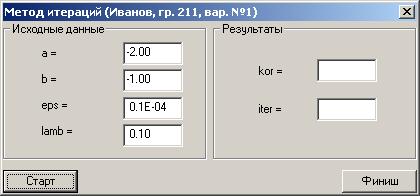
3.15. Нажмите на кнопку Старт. Результаты расчета появятся в соответствующих окнах панели приложения.
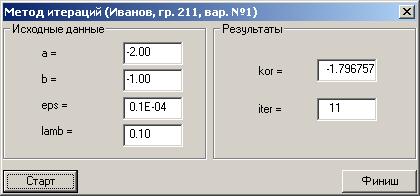
3.16. Проанализируйте результаты расчета, они должны совпадать с результатами в других средах программирования с заданной точностью (пять знаков после десятичной точки) и с помощью других методов. Обратите внимание на эффективность итерационного метода, показателем которой является количество затраченных итераций приближения к корню. Итерационный метод является не самым эффективным методом приближенного вычисления корня уравнения, но отличается простотой и очень популярен в инженерной практике. Нажмите кнопку Финиш для завершения приложения и оформите отчет о работе.
Варианты исходных данных
| № варианта | Определенный интеграл | № варианта | Определенный интеграл |
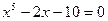
| 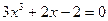
| ||
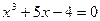
| 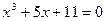
| ||
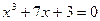
| 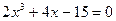
| ||
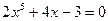
| 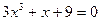
| ||
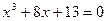
| 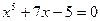
| ||
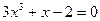
| 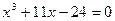
| ||
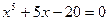
| 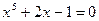
| ||
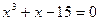
| 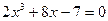
| ||

| 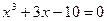
| ||
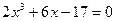
| 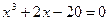
| ||
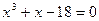
| 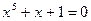
| ||
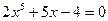
| 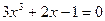
| ||
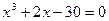
| 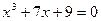
| ||
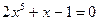
| 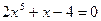
| ||
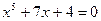
| 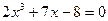
|
 2015-02-27
2015-02-27 606
606








