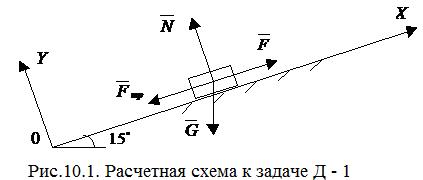
Задача Д-1. Телу массой m сообщена начальная скорость 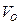 направленная вверх по наклонной плоскости, составляющей угол α с горизонтом, на тело действует сила
направленная вверх по наклонной плоскости, составляющей угол α с горизонтом, на тело действует сила 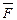 , направленная в туже сторону. Зная закон изменения силы
, направленная в туже сторону. Зная закон изменения силы 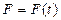 и коэффициентом трения скольжения
и коэффициентом трения скольжения 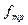 , определить скорость тела в моменты времени
, определить скорость тела в моменты времени 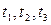 и проверить полученный результат для момента времени
и проверить полученный результат для момента времени 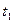 с помощью дифференцированного уравнения движения.
с помощью дифференцированного уравнения движения.
 | Дано: 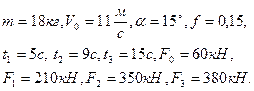 |
Решение:
По теореме об изменении количества движения имеем
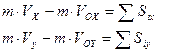 ,
,
где 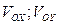 - проекции скорости в начале участка на оси координат,
- проекции скорости в начале участка на оси координат, 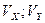 - проекции скорости в момент времени
- проекции скорости в момент времени 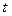 , (очевидно
, (очевидно 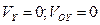 ).
).
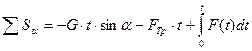 - сумма проекций импульсов сил, действующих на тело, на ось OX;
- сумма проекций импульсов сил, действующих на тело, на ось OX;
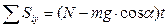 - сумма проекций импульсов сил на ось OY.
- сумма проекций импульсов сил на ось OY.
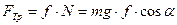 =>
=>
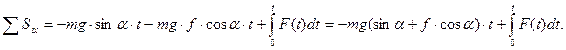
Обозначим 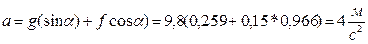 , тогда уравнение принимает вид:
, тогда уравнение принимает вид:
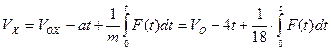 .
.
Полученное уравнение можно применит к каждому участку если считать, что 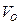 - скорость тела в начале рассматриваемого участка,
- скорость тела в начале рассматриваемого участка, 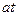 -время, отсчитываемое от начала рассматриваемого участка.
-время, отсчитываемое от начала рассматриваемого участка.
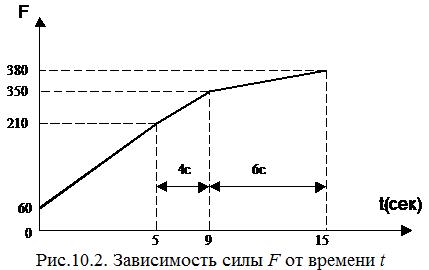
1) Участок №1
Здесь 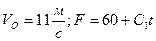 - зависимость силы F от времени t. Но при t=5 с
- зависимость силы F от времени t. Но при t=5 с 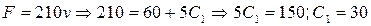 , то есть
, то есть 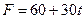
Находим импульс силы F.
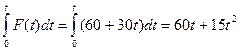
Уравнение принимает вид: 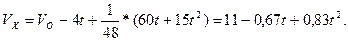
Проверим, возможно ли остановить тела на этом участке. Находим дискриминант квадратного трехчлена 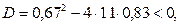 следовательно, при любых t
следовательно, при любых t 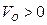 и значит останов невозможен. t=5c находим
и значит останов невозможен. t=5c находим 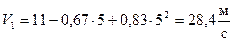
2) Участок №2
Здесь 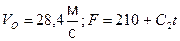 при
при
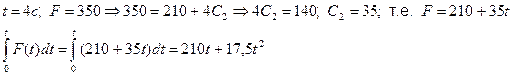 .
.
Уравнение имеет вид: 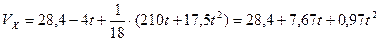 .
.
Здесь очевидно VX>0 при любых t, т.е. останов невозможен. При t=4c. Находим:
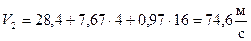 .
.
3) Участок №3
Здесь
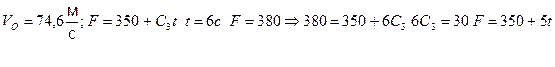
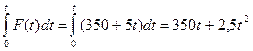 .
.
Уравнение имеет вид:
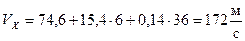 .
.
Дифференциальное уравнение движения тела на первом участке имеет вид:
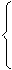
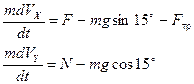 ,
,
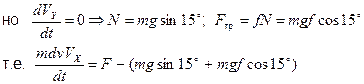
Делим на m и вводим обозначение 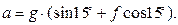 Получаем
Получаем 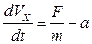
Интегрируя в пределах от 0 до t, получаем уравнение:
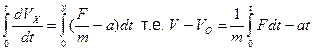
или
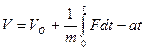 .
.
 2015-02-27
2015-02-27 1552
1552
