2014-02-09
5269
Кинематическое исследование механизмов.
Кинематический анализ плоского механизма. План скоростей и ускорений.
Лекция 10
Кинематическое исследование – исследование трёх величин – перемещения, скорости и ускорения какой-либо точки интересующего нас звена.
Рис.10.1
Цикл – время движения ведущего звена в машине, после которого
положение звеньев повторяется.
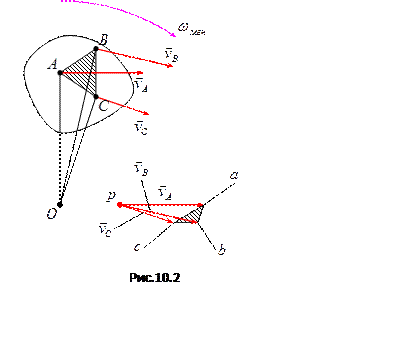
Представим себе плоское движение.
Модуль скорости точки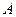 
можно определить по формуле:
,
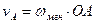а линия действия этого вектора будет перпендикулярная отрезку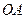 
.
Модуль скорости точки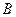 
можно определить по формуле:
,
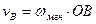а линия действия этого вектора будет перпендикулярная отрезку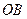 
.
Модуль скорости точки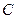 
можно определить по формуле:
,
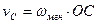а линия действия этого вектора будет перпендикулярная отрезку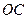 
.
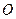- мгновенный центр вращения.
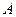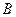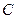Видно, что модули скоростей точек , и пропорциональны длинам отрезков 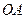, 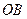и 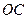, то есть:
.
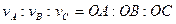Многоугольник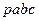 
подобен многоугольнику 
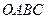, так как он образован взаимно перпендикулярными и пропорциональными прямыми. Поэтому рисунок 10.2 представляет собой план скоростей треугольника 
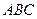, то есть треугольник 
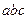является планом скоростей треугольника .
|
|
|
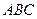План скоростей жёсткого звена – геометрическое место точек концов векторов абсолютных скоростей любых точек звена, если они построены из одной общей точки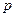 
, называемой полюсом плана скоростей.
План скоростей всегда строится в масштабе. В дисциплине «Теория машин и механизмов» масштаб имеет размерность, поэтому его принято называть масштабным коэффициентом: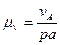 
, 
.
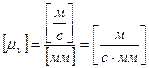План скоростей подобен самому звену, и повёрнут на девяносто градусов в сторону мгновенного вращения.
Если план скоростей жёсткого звена подобен своему звену, то план скоростей механизма не подобен самому механизму, так как в отличие от жёсткого звена механизм есть изменяемая подвижная система.
План скоростей механизма – совокупность планов скоростей отдельных звеньев, построенных из одной общей точки 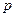, называемой полюсом плана скоростей.
Пример.
Дано: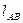 
, 
и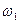 
.
Требуется определить: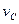 
.
Зададимся неким масштабным коэффициентом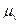 
.
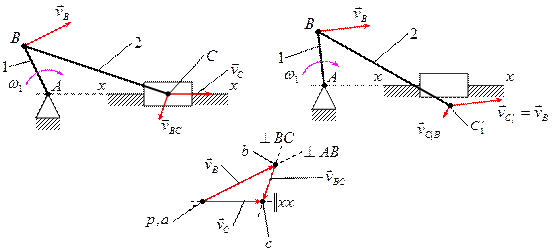
Рис.10.3
Для построения плана скоростей механизма существуют различные методы, наиболее распространённым из которых является метод векторных уравнений. Модуль скорости точки 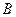можно определить по следующей формуле:
.
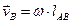Линия действия вектора скорости точки 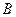перпендикулярна звену 
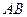, а сам вектор направлен в сторону вращения звена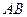
Допустим, что точка 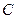не закреплена, и представим себе, что все точки звена 
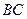совершают переносное движение со скоростью 
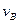, то есть 
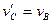. С одной стороны 
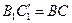, с другой стороны 
.
|
|
|
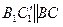Вернём точку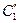 
на действительную траекторию 
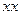, для чего придадим точке 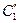скорость относительного вращательного движения около точки 
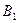со скоростью относительного движения 
.
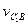На плане скоростей векторы, исходящие из полюса скоростей 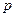являются векторами абсолютных скоростей соответствующих точек, а векторы, которые не проходят через полюс плана ускорений, являются относительных скоростей соответствующих точек. Отрезок 
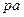является планом скоростей звена 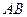, а отрезок 
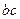является планом скоростей звена .
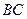10.2. Определение ускорений. Понятие о теореме подобия для определения ускорений отдельных точек звеньев.
Рассуждая аналогично теореме подобия для определения скоростей отдельных точек звеньев, очевидно, что план ускорений жёсткого звена подобен самому звену, и повёрнут на девяносто градусов.
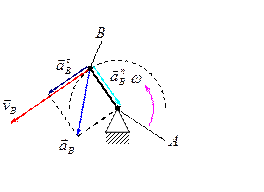
Полное ускорение можно найти геометрически просуммировав нормальное и тангенциальное ускорения, то есть: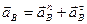 
.
Рис.10.4
Модуль вектора нормального ускорения точки 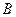можно найти по формуле: 
.
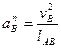Линия действия этого вектора будет перпендикулярна звену .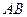
Модуль вектора тангенциального ускорения точки 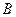можно найти по формуле: 
.
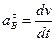Линия действия этого вектора будет параллельна звену .
