Метод секущих является комбинацией метода Ньютона и общей схемы исключения интервалов. Как уже отмечалось, равенство ¦  (x) = 0 является необходимым и достаточным условием глобального минимума выпуклой дифференцируемой функции ¦(x). Поэтому если на концах отрезка [ c; d ] производная ¦
(x) = 0 является необходимым и достаточным условием глобального минимума выпуклой дифференцируемой функции ¦(x). Поэтому если на концах отрезка [ c; d ] производная ¦  (x) имеет разные знаки, т.е. ¦
(x) имеет разные знаки, т.е. ¦  (с) ¦
(с) ¦  (d) < 0, то на интервале (a; b) найдется точка, в которой ¦
(d) < 0, то на интервале (a; b) найдется точка, в которой ¦  (x) обращается в нуль, и поиск точки минимума ¦(x) на [ c; d ] эквивалентен решению уравнения
(x) обращается в нуль, и поиск точки минимума ¦(x) на [ c; d ] эквивалентен решению уравнения
¦  (x) = 0, x Î(a; b) (5.11)
(x) = 0, x Î(a; b) (5.11)
Отсюда следует, что при ¦  (c) ¦
(c) ¦  (d) < 0 любой приближенный метод решения уравнения (5.11) можно рассматривать как метод минимизации выпуклой дифференцируемой функции ¦(x) на отрезке [ c; d ].
(d) < 0 любой приближенный метод решения уравнения (5.11) можно рассматривать как метод минимизации выпуклой дифференцируемой функции ¦(x) на отрезке [ c; d ].
Предположим, что в процессе поиска стационарной точки функции ¦(x) в интервале (a; b) обнаружены две точки c и d, в которых знаки производной различны. В этом случае алгоритм метода секущих позволяет аппроксимировать функцию ¦  (x) “секущей прямой” и найти точку, в которой секущая графика ¦
(x) “секущей прямой” и найти точку, в которой секущая графика ¦  (x) пересекает ось абцисс (рис. 5.14). Таким образом, следующее приближение к стационарной точке x
(x) пересекает ось абцисс (рис. 5.14). Таким образом, следующее приближение к стационарной точке x  определяется по формуле:
определяется по формуле:
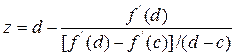 .
.
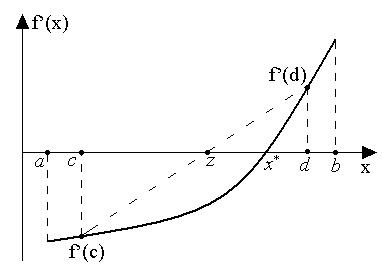
Рис. 5.12. Метод секущих
Если |¦  (z)| £ e, поиск следуетзакончить. В противном случае необходимо выбрать одну из точек c или d таким образом, чтобы знаки производной в этой точке и точке z были различны, а затем повторить основной шаг алгоритма. Например, в ситуации, изображенной на рис. 5.12., в качестве двух следующих точек должны быть выбраны точки z и d.
(z)| £ e, поиск следуетзакончить. В противном случае необходимо выбрать одну из точек c или d таким образом, чтобы знаки производной в этой точке и точке z были различны, а затем повторить основной шаг алгоритма. Например, в ситуации, изображенной на рис. 5.12., в качестве двух следующих точек должны быть выбраны точки z и d.
Легко видеть, что в отличие от метода средней точки метод секущих основан на исследовании не только знака, но и значений производной в пробных точках и поэтому в ряде случаев позволяет исключить более половины интервала поиска (см. рис. 5.12.).
Пример 5.7. Опять рассмотрим задачу из примера 5.5: минимизировать
¦(x) = 2 x 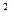 + (16/ x)
+ (16/ x)
в интервале 1 £ x £ 5.
¦  (x) =
(x) = 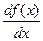 = 4 x -
= 4 x - 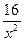 .
.
И т е р а ц и я 1.
Шаг 1. d = 5, c = 1, ¦  (d) = 19,36, ¦
(d) = 19,36, ¦  (c) = -12.
(c) = -12.
Шаг 2.
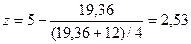 .
.
Шаг 3. ¦  (z) = 7,62> 0; положить d = 2,53.
(z) = 7,62> 0; положить d = 2,53.
И т е р а ц и я 2.
Шаг 2.
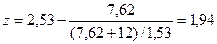 .
.
Шаг 3. ¦  (z) = 3,51> 0; положить d = 1,94. Итерации продолжаются до тех пор, пока не будет выполняться неравенство |¦
(z) = 3,51> 0; положить d = 1,94. Итерации продолжаются до тех пор, пока не будет выполняться неравенство |¦  (z)| £ e.
(z)| £ e.
 2015-02-04
2015-02-04 1329
1329