Метод Ньютона часто используется на завершающем этапе минимизации, когда x  – точка минимума грубо найдена другим, менее трудоемким методом и требуется найти x
– точка минимума грубо найдена другим, менее трудоемким методом и требуется найти x  с большой точностью. Кроме того, если функция ¦(x) содержит члены, включающие x в третьей и более высоких степенях, то непосредственное получение аналитического решения уравнения ¦
с большой точностью. Кроме того, если функция ¦(x) содержит члены, включающие x в третьей и более высоких степенях, то непосредственное получение аналитического решения уравнения ¦  (x) = 0 может оказаться затруднительным. В таких случаях используются приближенные методы последовательного поиска стационарной точки функции ¦(x). Ньютон разработал схему, ориентированную на нахождение корня нелинейного уравнения, которая позднее была уточнена Рафсоном.
(x) = 0 может оказаться затруднительным. В таких случаях используются приближенные методы последовательного поиска стационарной точки функции ¦(x). Ньютон разработал схему, ориентированную на нахождение корня нелинейного уравнения, которая позднее была уточнена Рафсоном.
В рамках схемы Ньютона – Рафсона предполагается, что ¦(x) – дважды дифференцируемая функция, причем ¦  (x) > 0 (это гарантирует выпуклость ¦(x)). Работа алгоритма начинается в точке x
(x) > 0 (это гарантирует выпуклость ¦(x)). Работа алгоритма начинается в точке x  , которая представляет начальное приближение координаты стационарной точки, или корня уравнения ¦
, которая представляет начальное приближение координаты стационарной точки, или корня уравнения ¦  (x) = 0. В очередной точке x
(x) = 0. В очередной точке x 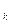 (k = 0,1,…) строится линейная аппроксимация функции ¦
(k = 0,1,…) строится линейная аппроксимация функции ¦  (x), и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения x
(x), и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения x 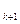 (рис. 5.10). Если точка x
(рис. 5.10). Если точка x 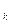 принята в качестве текущего приближения к стационарной точке, то уравнение
принята в качестве текущего приближения к стационарной точке, то уравнение
|
|
|
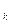 имеет вид
имеет вид y = ¦(x 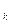 ) + ¦
) + ¦  (x
(x 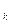 )(x - x
)(x - x 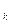 ).
).
Точка x = x 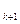 , найденная из условия y = 0, определяется формулой
, найденная из условия y = 0, определяется формулой
x 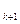 = x
= x 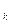 - ¦(x
- ¦(x 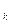 )/¦
)/¦  (x
(x 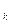 ).
).
Полагая ¦(x) = ¦  (x), тогда для решения уравнения ¦
(x), тогда для решения уравнения ¦  (x) = 0 необходимо построить последовательность
(x) = 0 необходимо построить последовательность
x 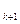 = x
= x 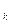 -
- 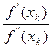 , k = 0,1,…, (5.10)
, k = 0,1,…, (5.10)
где x  – точка, выбранная в качестве начального приближения.
– точка, выбранная в качестве начального приближения.
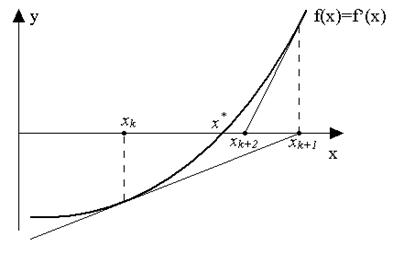
Рис. 5.10. Метод Ньютона – Рафсона (сходимость)
В зависимости от выбора начальной точки и вида функции алгоритм может, как сходиться к истинной стационарной точке, так и расходиться, что отражено на рис. 5.11. Если начальная точка расположена правее x  , то получаемые в результате последовательных приближений точки удаляются от стационарной точки x
, то получаемые в результате последовательных приближений точки удаляются от стационарной точки x  .
.
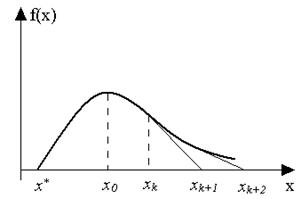
Рис. 5.11. Метод Ньютона – Рафсона (отсутствие сходимости)
Оценка скорости сходимости может быть сформулирована следующим образом. Пусть ¦(x) – дважды дифференцируемая на E 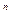 функция, причем ¦
функция, причем ¦  (x) ³ m > 0 при всех x Î E и ¦
(x) ³ m > 0 при всех x Î E и ¦  (x) удовлетворяет условию Липшица на X с константой L. Тогда, если начальное приближение x
(x) удовлетворяет условию Липшица на X с константой L. Тогда, если начальное приближение x  удовлетворяет условию
удовлетворяет условию
q = 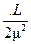
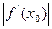 < 1,
< 1,
то последовательность (5.11) сходится к единственной точке минимума x  функции ¦(x) на X, причем
функции ¦(x) на X, причем
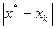 £
£ 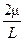 q
q 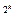 , k = 0,1,…
, k = 0,1,…
Вычисления по формуле (5.10) производят до тех пор, пока не выполнится неравенство |¦  (x
(x 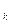 )| £ e, после чего полагают x
)| £ e, после чего полагают x  » x
» x 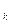 , ¦
, ¦  »¦(x
»¦(x 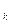 ).
).
Пример 5.5. Рассмотрим следующую задачу: минимизировать
¦(x) = 2 x 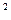 + (16/ x), e = 0,05.
+ (16/ x), e = 0,05.
Для того чтобы определить стационарную точку функции ¦(x), воспользуемся методом Ньютона – Рафсона, положив x 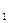 = 1:
= 1:
¦  (x) = 4 x - (16/ x
(x) = 4 x - (16/ x 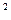 ), ¦
), ¦  (x) = 4 + (32/ x
(x) = 4 + (32/ x 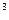 ).
).
И т е р а ц и я 1. x 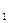 = 1, ¦
= 1, ¦  (x
(x 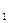 ) = -12, ¦
) = -12, ¦  (x
(x 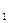 ) = 36, x
) = 36, x 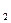 = 1-(-12/36) = 1,33.
= 1-(-12/36) = 1,33.
И т е р а ц и я 2. x 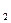 = 1,33, ¦
= 1,33, ¦  (x
(x 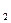 ) = -3,73, ¦
) = -3,73, ¦  (x
(x 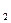 ) = 17,6, x
) = 17,6, x 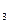 =1,33-
=1,33- 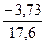 = 1,54.
= 1,54.
И т е р а ц и я 3. х 3 = 1,54, 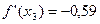 ,
,
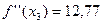 ,
, 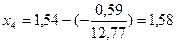 .
.
И т е р а ц и я 4. 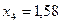 ,
, 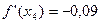 ,
,
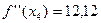 ,
, 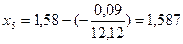 .
.
И т е р а ц и я 5. 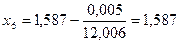 .
.
Так как 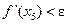 , то
, то 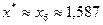 ,
, 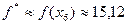 .
.
 2015-02-04
2015-02-04 2372
2372








