На этом этапе сначала выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. Обычно поиск граничных точек такого интервала проводится с помощью эвристических методов поиска. В этом случае (k +1)-я пробная точка определяется по рекуррентной формуле (метод Swann W.H.)
x 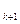 = x
= x 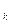 +2
+2 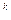 D, k = 0, 1, 2,…,
D, k = 0, 1, 2,…,
где x  – произвольно выбранная начальная точка; D − подбираемая некоторым способом величина шага. Знак D определяется путем сравнения значений ¦(x
– произвольно выбранная начальная точка; D − подбираемая некоторым способом величина шага. Знак D определяется путем сравнения значений ¦(x  ), ¦(x
), ¦(x  + |D|) и ¦(x
+ |D|) и ¦(x  − |D|). Если
− |D|). Если
¦(x  - |D|) ³ ¦(x
- |D|) ³ ¦(x  ) ³ ¦(x
) ³ ¦(x  + |D|),
+ |D|),
то, согласно предположению об унимодальности, точка минимума должна располагаться правее точки x  и величина D выбирается положительной. Если изменить знаки неравенств на противоположные, то D следует выбирать отрицательной. Если же
и величина D выбирается положительной. Если изменить знаки неравенств на противоположные, то D следует выбирать отрицательной. Если же
¦(x  - |D|) ³ ¦(x
- |D|) ³ ¦(x  ) £ ¦(x
) £ ¦(x  + |D|),
+ |D|),
то точка минимума лежит между x  − |D| и x
− |D| и x  + |D| и поиск граничных точек завершен. Случай, когда
+ |D| и поиск граничных точек завершен. Случай, когда
¦(x  - |D|) £ ¦(x
- |D|) £ ¦(x  ) ³ ¦(x
) ³ ¦(x  + |D|),
+ |D|),
противоречит предположению об унимодальности.
Пример 5.2. Рассмотрим задачу минимизации функции ¦(x) = (100- x) 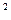 при заданной начальной точке x
при заданной начальной точке x  = 30 и величине шага |D| = 5.
= 30 и величине шага |D| = 5.
Знак D определяется на основе сравнения значений
¦(x  ) = ¦(30) = 4900,
) = ¦(30) = 4900,
¦(x  + |D|) = ¦(35) = 4225,
+ |D|) = ¦(35) = 4225,
¦(x  − |D|) = ¦(25) = 5625.
− |D|) = ¦(25) = 5625.
Так как
¦(x  − |D|) ³ ¦(x
− |D|) ³ ¦(x  ) ³ ¦(x
) ³ ¦(x  +|D|),
+|D|),
то величина D должна быть положительной, а координата точки минимума x  должна быть больше 30. Имеем x
должна быть больше 30. Имеем x 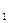 = x
= x  + D = 35. Далее
+ D = 35. Далее
x 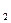 = x
= x 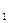 + 2D = 45, ¦(45) = 3025 < ¦(x
+ 2D = 45, ¦(45) = 3025 < ¦(x 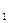 ),
),
откуда x  > 35.
> 35.
x 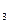 = x
= x 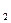 +2
+2 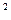 D = 65, ¦(65) = 1225 < ¦(x
D = 65, ¦(65) = 1225 < ¦(x 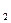 ),
),
откуда x  > 45.
> 45.
x 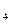 = x
= x 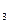 +2
+2 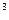 D = 105, ¦(105) = 25 < ¦(x
D = 105, ¦(105) = 25 < ¦(x 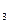 ),
),
откуда x  >65.
>65.
x 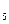 = x
= x 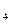 + 2
+ 2 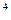 D= 185, ¦(185) = 7225 > ¦(x
D= 185, ¦(185) = 7225 > ¦(x 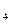 ),
),
следовательно, x  < 185.
< 185.
Таким образом, шесть шагов вычислений x  позволили выявить интервал 65 £ x
позволили выявить интервал 65 £ x  £ 185, в котором расположена точка x
£ 185, в котором расположена точка x  . Эффективность поиска граничных точек зависит от величины шага D. Если D велико – получаем грубые оценки координат граничных точек. Если D мало, то может потребоваться большой объем вычислений.
. Эффективность поиска граничных точек зависит от величины шага D. Если D велико – получаем грубые оценки координат граничных точек. Если D мало, то может потребоваться большой объем вычислений.
 2015-02-04
2015-02-04 797
797








