2015-02-04
432
Условие задачи: Для расчетной схемы, представленной на рис. 2.5 записать матричное уравнение узловых напряжений и рассчитать значения узловых напряжений методом Гаусса.
Исходные данные:
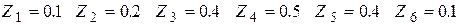- сопротивления
ветвей;
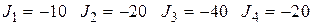- задающие токи, моделирующие
подключение нагрузки.
Расчет начинается с формирования уравнения состояния по расчетной схеме:
1. 
Составим матрицу инциденций 1-го рода.
1 2 3 4 5 6
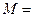
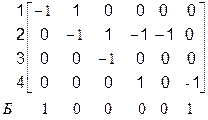
При правильном составлении матрицы М строка, соответствующая балансирующему узлу, дополняет каждый столбец до нуля.
2.Составим транспонированную матрицу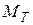 
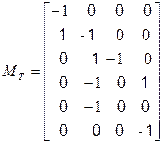
3.Определяем матрицу узловых проводимостей
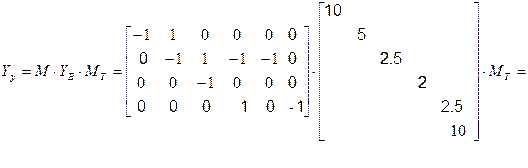
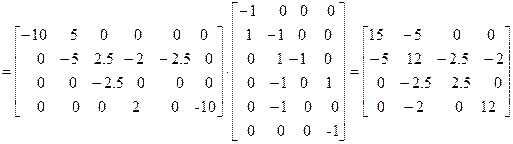
В матричной форме уравнение узловых напряжений имеет вид:
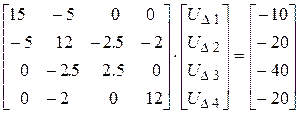(2.5)
5. Перейдем к системе уравнений:
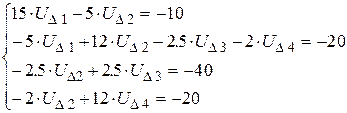(2.6)
Далее, используя уравнения узловых напряжений, можно провести расчет установившегося режима в следующем порядке:
1. Решая систему уравнений вида (1.12), определяются значения узловых напряжений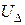 
. Произведем расчет с помощью метода Гаусса.
Прямой ход Гаусса состоит из однотипных шагов, связанных с формированием из матрицы коэффициентов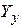 
верхней треугольной матрицы.
Шаг 1. Получим первое ключевое уравнение, для чего разделим первое уравнение системы (2.5) на коэффициент при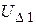 
, а затем исключим 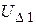из всех уравнений, расположенных ниже ключевого.
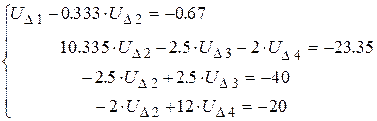(2.7)
Шаг 2. Принимаем за ключевое второе уравнение (разделим все коэффициенты на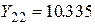 
) и исключим 
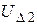из уравнений ниже ключевого.
Преобразованная система, начиная с ключевого уравнения имеет вид:
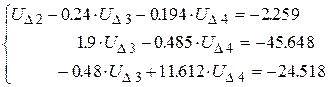(2.8)
Шаг 3. Принимаем за ключевое третье уравнение и исключаем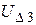 
из всех уравнений ниже ключевого, преобразованная система, начиная с ключевого уравнения имеет вид:
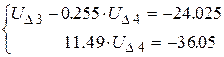(2.9)
Шаг 4. Выбираем четвертое ключевое уравнение:
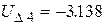(2.10)
Обратный ход Гаусса:
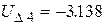
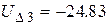
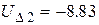
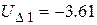
Анализ точности расчета: Производится расчет невязок по исходной системе уравнений:
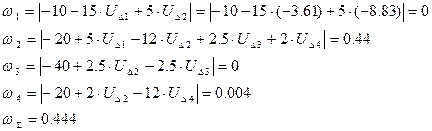(2.11)
2. Из уравнения связи параметров режима [ 1 ] находятся падения напряжений в ветвях
. 
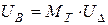(2.12)
3. Из уравнения закона Ома (1.1) определяются токи в ветвях схемы
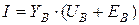. (2.13)
4.По известным значениям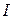 
и 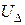определяются остальные параметры режима 
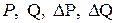и т.д.
