Основные формы уравнений состояния ЭЭС: обобщенное уравнение состояния, уравнения узловых напряжений, контурные уравнения подробно описаны в [1].
В качестве примера линейных математических моделей рассмотрим наиболее широко используемые на практике формы уравнений состояния - обобщенное уравнение состояния и уравнение узловых напряжений в матричной форме или в виде системы уравнений, которые описывают нормальный режим работы ЭЭС.
Обобщенное уравнение состояния в матричной форме имеет вид:
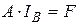 , (2.1)
, (2.1)
где 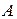 - объединенная матрица коэффициентов, которая включает в себя две матрицы
- объединенная матрица коэффициентов, которая включает в себя две матрицы 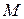 ,
, 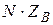 и имеет следующую структуру:
и имеет следующую структуру:
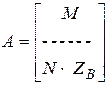
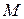 - матрица инцидениций 1-го рода, предназначена для описания структурных связей узлов и ветвей в расчетной схеме. (
- матрица инцидениций 1-го рода, предназначена для описания структурных связей узлов и ветвей в расчетной схеме. (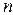 - количество узлов,
- количество узлов, 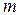 - количество ветвей);
- количество ветвей);
Структура:
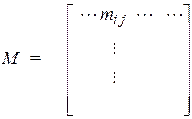
Правило формирования: каждый элемент матрицы 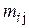 , располагается на пересечении строки
, располагается на пересечении строки 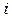 (номер узла) и столбца
(номер узла) и столбца 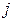 (номер строки), его значение определяется следующим образом:
(номер строки), его значение определяется следующим образом:
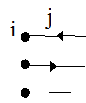
|
-1, если ветвь 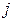 входит в узел
входит в узел 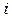
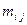 = 1, если ветвь
= 1, если ветвь 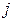 выходит из узла
выходит из узла 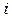
0, если ветвь 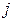 не соединена с узлом
не соединена с узлом 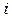 .
.
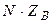
 -произведение двух матриц:
-произведение двух матриц:
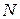 - структурная матрица инциденций второго рода, отражающая связь ветвей
- структурная матрица инциденций второго рода, отражающая связь ветвей 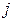 в независимые контуры
в независимые контуры 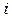 .
.
Структура:
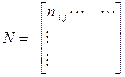
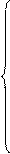 Правило формирования:
Правило формирования:
|
-1, если направление ветки 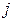
противоположно направлению обхода контура 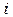
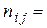 1, если направление ветки
1, если направление ветки 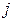 совпадает с
совпадает с
направлением обхода контура 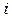
0, если ветвь не входит в контур 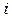
 - матрица сопротивлений ветвей.
- матрица сопротивлений ветвей.
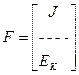 - объединенная матрица свободных членов, включающая в себя:
- объединенная матрица свободных членов, включающая в себя:
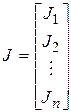 - вектор задающих токов;
- вектор задающих токов; 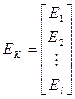 - вектор ЭДС контуров.
- вектор ЭДС контуров.
При использовании обобщенного уравнения состояния расчет установившегося режима ЭЭС производится в следующем порядке: вначале определяются токи в ветвях схемы 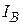 , а затем рассчитываются падения напряжения в ветвях
, а затем рассчитываются падения напряжения в ветвях 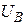 , напряжения в узлах
, напряжения в узлах 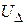 , потоки активной и реактивной мощностей
, потоки активной и реактивной мощностей 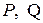 и т.д. Пример расчета приведен ниже при описании реализации в среде Mathcad.
и т.д. Пример расчета приведен ниже при описании реализации в среде Mathcad.
Общий вид уравнения узловых напряжений [1,2]:
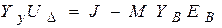 , (2.2)
, (2.2)
где 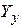 - матрица узловых проводимостей;
- матрица узловых проводимостей;
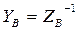 - матрица проводимостей ветвей, обратная матрице сопротивлений ветвей
- матрица проводимостей ветвей, обратная матрице сопротивлений ветвей 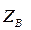 ;
;
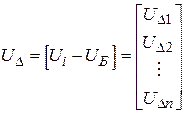
 - матрица узловых напряжений;
- матрица узловых напряжений;
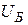 - базисное напряжение балансирующего узла.
- базисное напряжение балансирующего узла.
Для большинства реальных схем замещения нагрузка и генерация мощности моделируются с помощью задающих токов 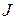 , поэтому ЭДС в ветвях отсутствует. Тогда (при
, поэтому ЭДС в ветвях отсутствует. Тогда (при 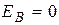 ) уравнение узловых напряжений имеет вид:
) уравнение узловых напряжений имеет вид:
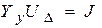 , (2.3)
, (2.3)
Матрица узловых проводимостей рассчитывается по формуле:
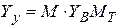 , (2.4)
, (2.4)
где
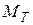 - транспонированная матрица инциденций первого рода;
- транспонированная матрица инциденций первого рода;
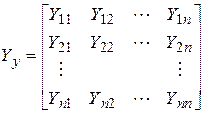 — матрица узловых проводимостей.
— матрица узловых проводимостей.
Структура 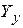 определяется физическим смыслом ее элементов:
определяется физическим смыслом ее элементов:
· на главной диагонали расположены собственные проводимости узлов 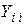 , равные сумме проводимостей ветвей, соединенных с узлом
, равные сумме проводимостей ветвей, соединенных с узлом 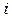 ;
;
· симметрично относительно главной диагонали расположены взаимные проводимости 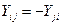 (со знаком минус), которые равны проводимости ветви, находящейся между узлами
(со знаком минус), которые равны проводимости ветви, находящейся между узлами 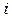 и
и 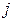 , или нулю при отсутствии связи между узлами.
, или нулю при отсутствии связи между узлами.
Матрица 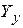 является симметричной и слабо заполненной, т.е. содержит большое число нулевых элементов. Эти свойства позволяют реализовать на ЭВМ эффективные алгоритмы расчета режимов с учетом слабой заполненности массивов.
является симметричной и слабо заполненной, т.е. содержит большое число нулевых элементов. Эти свойства позволяют реализовать на ЭВМ эффективные алгоритмы расчета режимов с учетом слабой заполненности массивов.
Использование уравнений узловых напряжений приводит к следующему порядку расчета режима ЭС: в начале определяются значения напряжений в узлах схемы 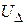 , затем рассчитываются токи
, затем рассчитываются токи 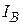 и падения напряжения
и падения напряжения 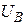 в ветвях схемы, потоки активной и реактивной мощности
в ветвях схемы, потоки активной и реактивной мощности 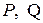 , потери мощности
, потери мощности 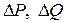 в электрической сети и т.д.
в электрической сети и т.д.
 2015-02-04
2015-02-04 671
671








