В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, причем возможны различные формы таких систем, например:
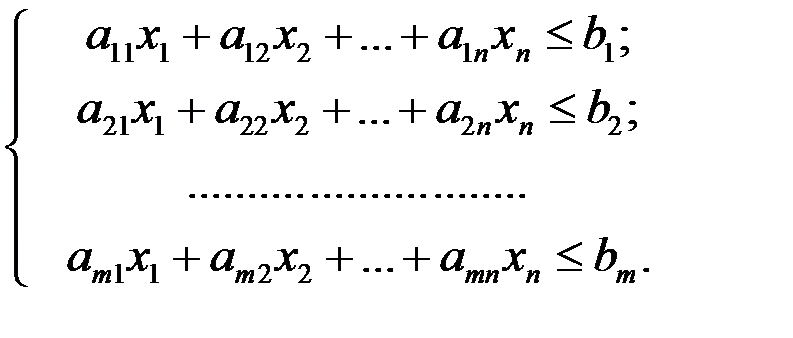 (4.2)
(4.2)
или
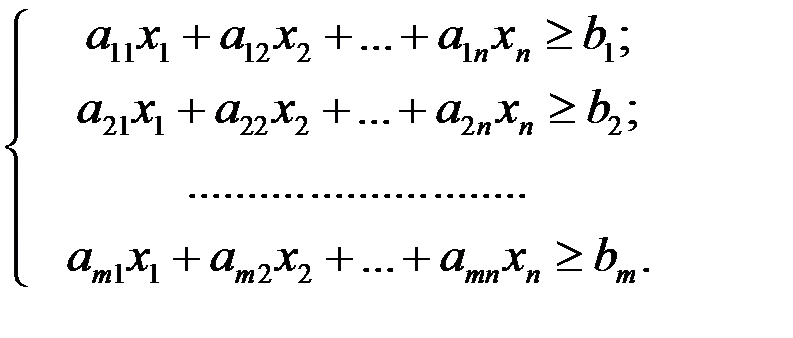 (4.3)
(4.3)
Наконец, система ограничений может быть смешанной: часть ограничений - неравенства типа (4.2), часть — типа (4.3), часть задана в виде уравнений.
Однако любую систему ограничений можно привести к системе уравнений вида (4.1). Для этого достаточно к левой части каждого неравенства (4.2) прибавить (отнять, если система задана в виде (4.3)) какое-то неотрицательное число - добавочную переменную, с тем чтобы каждое неравенство обратилось в уравнение.
Пусть система ограничений задана неравенствами вида (4.2). Прибавим к левой части каждого неравенства соответствующую добавочную неотрицательную переменную (хп+1, хп+2...,хп+т), где xn+j > 0 (i = 1, 2,...m). В результате вместо системы неравенств (4.2) получим эквивалентную систему уравнений:
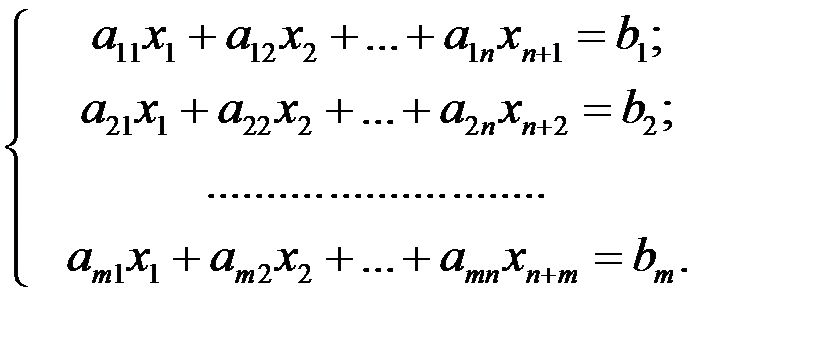 (4.4)
(4.4)
т. е. систему ограничений, аналогичную системе (4.1).
В случае смешанных систем ограничений, т. е. если в системе есть неравенства видов (4.2) и (4.3), а часть ограничений задана в виде уравнений, число добавочных переменных меньше т, а именно оно равно m -t, где m - общее число ограничений системы, a t- число ограничений в виде уравнений.
Таким образом, как бы ни были первоначально заданы ограничения задачи линейного программирования, их всегда можно привести к системе линейных уравнений, используя для этой цели добавочные переменные, т.е. свести задачу к канонической.
Известно, что система m линейных уравнений с n переменными может быть как совместной, так и несовместной, а уравнения системы - как зависимыми, так и независимыми.
Несовместность системы означает, что ее уравнения противоречивы. В этом случае система не имеет ни одного решения, а следовательно, не имеет решения и задача линейного программирования.
Будем считать, что все m уравнений системы (4.1) линейно независимы. В противном случае из системы можно исключить часть уравнений так, чтобы уравнения системы стали линейно независимыми.
Совместная система m линейных уравнений с п переменными (m <n) имеет бесчисленное множество всевозможных решений, в том числе и допустимых (не имеющих отрицательных компонент), а количество ее базисных решений не превышает числа 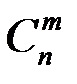 .
.
Напомним также, что допустимым базисным решением является решение, содержащее m неотрицательных основных (базисных) переменных (компонент) и n - m неосновных (небазисных, или свободных) переменных. Неосновные переменные в базисном решении равны нулю. Основные же переменные, как правило, отличны от нуля, т.е. являются положительными числами.
Если хотя бы одна из основных переменных принимает нулевое значение, то соответствующее базисное решение называется вырожденным.
За основные переменные можно принять любые m переменных, если только определитель, составленный из коэффициентов при них, отличен от нуля.
Так как компоненты оптимального решения задачи линейного программирования не могут быть отрицательными, то поиски этого решения нужно ограничить только допустимыми решениями системы ограничений.
Пример 4.1. Для производства двух видов сельскохозяйственной продукции с сенокосов и пашни требуется четыре вида ресурса: минеральные удобрения; оросительная вода; площадь сельскохозяйственных угодий; трудовые ресурсы. Необходимо составить такой план производства указанных видов продукции, который обеспечит получение её максимального количества в стоимостном выражение в условиях ограниченности ресурсов. Данные приведены в таблице 4.1.
Таблица 4.1 – Данные к примеру 4.1
| Вид ресурса | Запасы ресурса | Число единиц ресурса необходимых для производства единицы продукции | |
| сенокос | пашня | ||
| I | |||
| II | |||
| III | |||
| IV | |||
| Стоимость реализации единицы продукции у.ед. |
Дадим математическую формулировку задачи. Пусть х 1и х 2 - соответственно количество продукции с сенокосов и пашни, запланированных к производству. Так как количество ресурсов по каждому виду ограничено, то должны выполняться следующие неравенства:
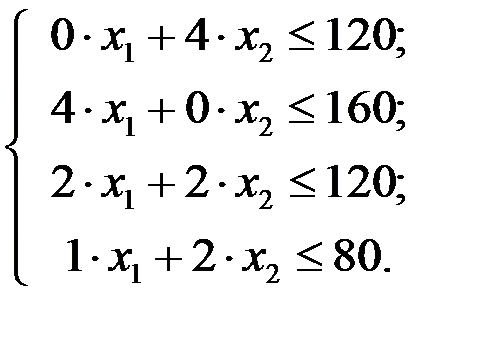
Эта система неравенств и является системой ограничений данной задачи. Целевая функция, выражающая стоимость реализации единицы продукции, имеет вид 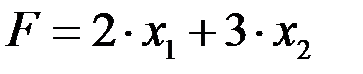 .
.
Задача сводится к нахождению максимума функции при ограничениях:
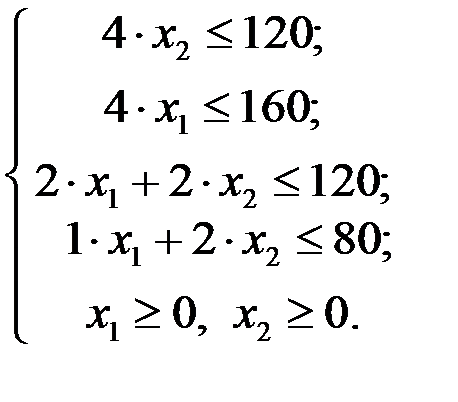
Для сведения системы ограничений-неравенств к системе уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные х 3, х 4, х 5, х 6. В условиях данной задачи они имеют конкретное экономическое содержание, а именно выражают объем остатков ресурсов каждого вида после выполнения плана по выпуску продукции. После введения добавочных переменных получим систему уравнений
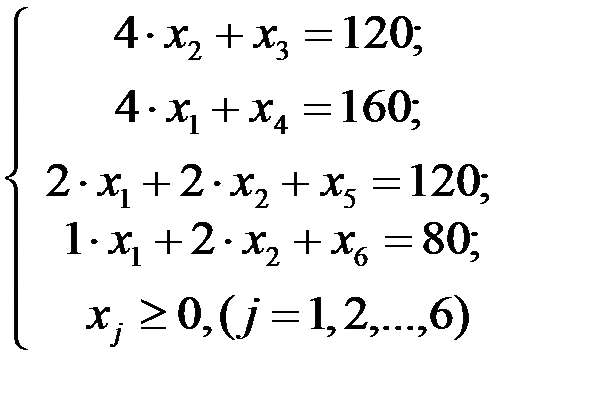
 2015-02-27
2015-02-27 614
614








