Экономико-математическая модель транспортной задачи

Транспортная задача имеет специфическую экономико-математическую модель и решается не универсальным симплексным методом, а с помощью распределительного метода и его различных модификаций.

Простейшими транспортными задачами являются задачи о перевозках некоторого однородного груза из пунктов отправления (от поставщиков) в пункты назначения (к потребителям) при обеспечении минимальных затрат на перевозки.

Обычно начальные условия таких задач записывают в таблицу. Например, для k поставщиков и i потребителей такая таблица имеет следующий вид.

Таблица 6.1 - Начальные условия транспортной задачи

Постав­щики

Мощности поставщиков

Потребители и их спрос

j

l

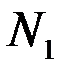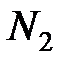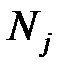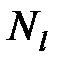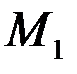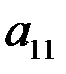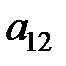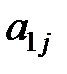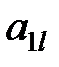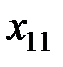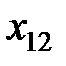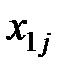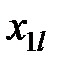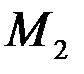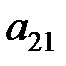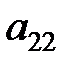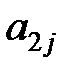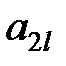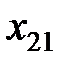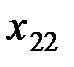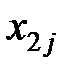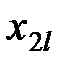i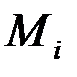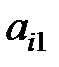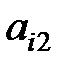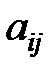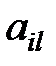

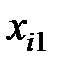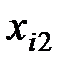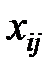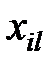k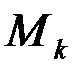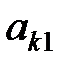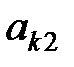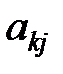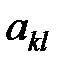

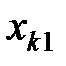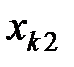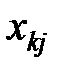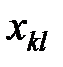Здесь показатели 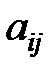означают затраты на перевозку единицы груза от i -го поставщика (i = 1, 2,…, k) к j - му потребителю (j = 1, 2, …, l), 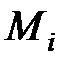– мощность i - го поставщика в планируемый период, N_j – спрос j - го потребителя на этот же период.

Обозначим через 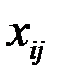поставку (количество груза), которая планируется к перевозке от i - го поставщика к j - му потребителю. Математически задача сводится к нахождению минимума целевой функции, выражающей суммарные затраты на перевозку всего груза, т. е. функции

,

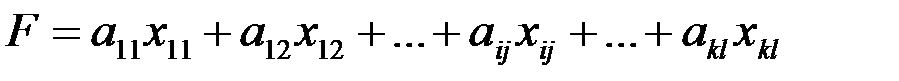при ограничениях

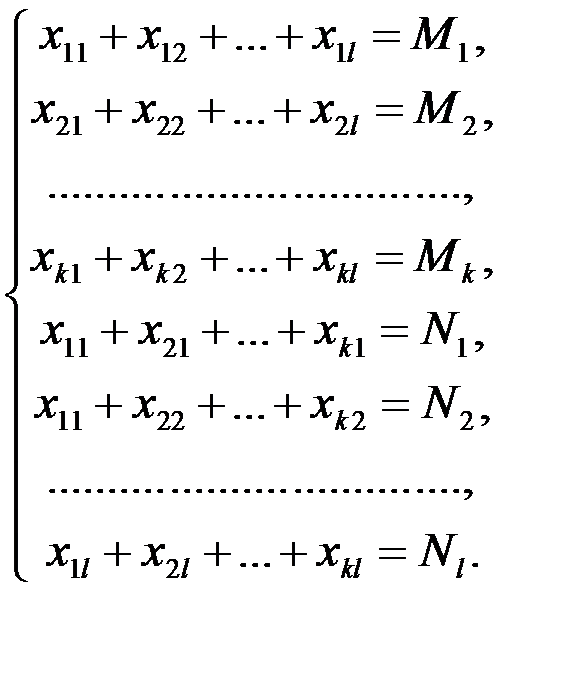(6.1)

Если к ограничениям (6.1) добавить еще одно:

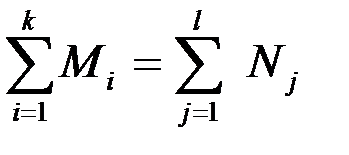(6.2)

т. е. суммарная мощность поставщиков равна суммарному спросу по­требителей, то соответствующая модель задачи называется закрытой.

Задачам, в которых ограничение (6.2) отсутствует, т. е. 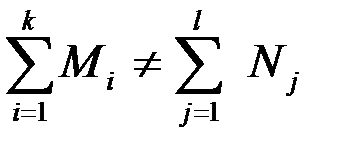первоначально соответствует открытая модель.

Отметим некоторые особенности экономико-математической модели транспортной задачи по сравнению с моделями задач линейного программирования, рассмотренных в предыдущих главах.

Система ограничений (6.1) сразу имеет вид уравнений, поэтому отпадает необходимость вводить добавочные переменные.

Матрица коэффициентов при переменных в системе (6.1) состоит только из единиц и нулей.

Система ограничений (6.1) включает k уравнений, связывающих поставки I -гo поставщика с мощностью М_l (i = 1, 2,…, k) этого поставщика, и l уравнений, связывающих поставки j -му потребителю со спросом N_j (j = 1, 2, …, l) этого потребителя. Заметим, что число k равно числу строк исходной таблицы, а число l - числу столбцов.

Число переменных 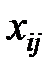, входящих в целевую функцию и в систему уравнений (6.1), равно произведению kl,т. е. числу клеток таблицы.

Таким образом, система ограничений (6.1) есть система из k + l уравнений с kl переменными.

Специфичность экономико-математической модели транспортной задачи привела к появлению особого метода ее решения – распределительного метода, а в дальнейшем – к различным модификациям этого метода.

Однако все теоретические предпосылки, которые лежат в основе симплексного метода, сохраняются.

Любое решение транспортной задачи 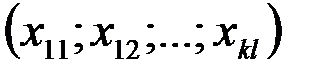называется распределением поставок. Так как поставки не могут быть отрицательными, то речь может идти только о допустимых решениях.

Оптимальному решению транспортной задачи соответствует оптимальное распределение поставок, при котором целевая функция 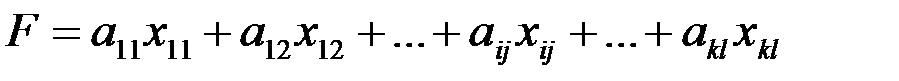достигает своего минимума.

В ходе решения задачи и нужно получить это оптимальное распределение поставок, которому соответствует какое-то допустимое базисное решение системы ограничений (17.1).

При распределительном методе решения транспортной задачи по­следовательно используются расчетные таблицы, соответствующие тому или иному шагу решения. Каждая такая таблица включает определенное распределение поставок. Так как распределение поставок должно соответствовать базисному решению, то и клетки таблицы должны соответствовать основным (положительным) и неосновным (равным нулю) переменным.

На практике это сводится к тому, что в клетки, соответствующие основным переменным, записывают поставки, а клетки, которым соответствуют неосновные, т. е. равные нулю, переменные, остаются не заполненными (свободными).

Замечание. Условимся использовать следующий способ заполнения клеток: в верхнем левом углу записываем показатель затрат (в последующих таблицах – оценки), а в нижнем правом – поставки.

Число заполненных клеток определяется числом основных переменных системы ограничений (6.1), а последнее равно числу линейно независимых уравнений системы.

Если решение задач симплексным методом означало переход от одного базисного решения к другому, пока не было найдено оптимальное решение или не был сделан вывод о несовместности системы ограничений, то решение транспортной задачи состоит в переходе от одного распределения поставок к другому распределению: от одной таблицы к другой. Новое распределение поставок должно снижать или, по крайней мере, не увеличивать общую стоимость затрат на перевозки. Перераспределение поставок должно осуществляться до тех пор, пока не будет найдено оптимальное распределение поставок.

Чтобы осуществлять переход от одного распределения поставок к другому, нужно иметь исходное (первоначальное) распределение поставок.