Метод математической индукции

Законы логики

Известно, что новые знания приобретаются человеком либо опытным путем, либо путем рассуждений. Все рассуждения подчиняются определенным правилам, называемым «законами логики» (тождественно-истинными формулами). Запишем некоторые из них в виде равносильностей формул исчисления высказываний:

1. А ⇔ А (закон тождества);

2. ( 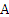& 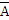) ⇔ 0 (закон противоречия);

3. А ∨ 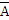⇔ 1 (закон исключенного третьего);

4. А → В ⇔ 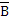→ 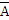(закон контрапозиции);

5. 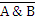⇔ A ∨ В (1-ый закон де Моргана);

6. 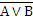⇔ А & В (2-ый закон де Моргана);

7. 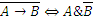(закон отрицания импликации);

8. (А → В) & (В → С) → (А → С) ⇔ 1 (закон силлогизма);

9. А & (А→В)→ В ⇔ 1 (закон заключения).

Закон противоречия требует, чтобы в рассуждениях не могли быть одновременно истинны некоторое высказывание и его отрицание; закон исключенного третьего состоит в том, что хотя бы одно из высказываний истинно: высказывание А или его отрицание .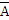

Полезно знать ряд законов, связанных с логикой предикатов:

10. 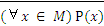⇔ ( 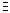х ∈ М) ;

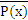11. 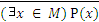⇔ ( 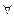x ∈ М) ;

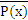12. 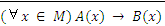⇔ ( 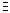х ∈ М) A(x) & );

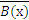13. ( 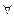х ∈ M) (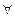 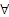y ∈ M) А(х, у)⇔ ( 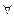y ∈ M) ( 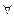x ∈ M) А(х, у).

Закон 10 отражает тот факт, что высказывания: «не всякий x обладает свойством Р» и «существует x, не обладающий свойством Р» ― имеют одинаковый смысл.

Закон 12 часто используется в тех случаях, когда опровергаются какие-то утверждения, и приводится контрпример, то есть приводится пример объекта из данного множества, удовлетворяющий условию и не удовлетворяющий заключению утверждения. Пусть нужно опровергнуть утверждение:

А(х) → В(х) 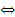«Если углы равны, то они вертикальные». Для этого достаточно привести пример равных, но не вертикальных углов, например, все прямые углы равны между собой, но не все они вертикальные.

Некоторые из указанных законов лежат в основе наиболее распространенных схем рассуждений (правил вывода).

Например:

1. «Все натуральные числа ― целые; все целые числа ― рациональные. Следовательно, все натуральные числа ― рациональные».

2. «Все квадраты ― ромбы; все ромбы ― параллелограммы. Следовательно, все квадраты параллелограммы».

Про эти два рассуждения можно сказать, что они имеют одну и ту же форму или структуру, построены по одной схеме:

Все А есть В, все В есть С: Все А есть С (основанной на законе силлогизма).

Если в эту форму вместо А, В, С подставить другие суждения, то все они будут иметь одинаковую форму. При этом, если посылки будут истинными, то и заключение будет истинно «по форме».

Отыскание и описание подобных правильных схем рассуждений составляет предмет формальной логики ― науки, создателем которой считают греческого философа Аристотеля (384–332 г. до н.э.).

Рассмотрим некоторые наиболее распространенные правильные схе­мы рассуждений, называемые также правилами вывода.

1. Правило заключения (Modus Ponens ― M.P.) (основано на законе заключения):

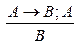
Почему эта схема надежна? Если предположить, что посылки истинны, то есть [А→В] =1, [А] =1, то из определения импликации следует, что [В] = 1. Это означает, что о чем бымы ни рассуждали по этой схеме, если мы исходим из истинных посылок, то никогда не придем к ложному заключению.

Поскольку в математике важно уметь анализировать предложения с кванторами, то приведем кванторный аналог указанного правила:

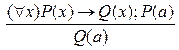
Это правило действует всюду, где приходится применять общие положения в частных случаях.

Например: «Если функция f(x) ― нечетная, то ее график симметричен относительно начала координат. Функция f(x) = х³ ― нечетная, следовательно, ее график симметричен относительно начала координат».

А вот схема рассуждения

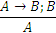
ненадежна, так как, если посылки истинны, то заключение может быть и ложным по определению импликации. Приведем еще примеры правильных схем рассуждений:

2. ;

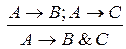3. ;

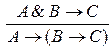4. 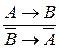― правило контрапозиции;

5. 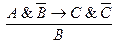― схема доказательства методом от «противного».

На практике она имеет различные вариации:

а) если 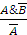, то говорят: «...что противоречит условию»;

б) если 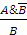, то говорят: «...что противоречит предположению»;

в) если 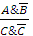, то говорят: «... что противоречит ранее доказанной теореме (или аксиоме)».

В арифметике в качестве метода доказательства широко применяется так называемый метод математической индукции. В предикатной форме схема доказательства этим методом утверждений, зависящих от натурального n, имеет следующий вид:

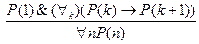
и называется принципом математической индукции.

В этой схеме Р(n) ― любой одноместный предикат, заданный на множестве N натуральных чисел и удовлетворяющий условиям:

а) Р(1) ― истинно;

б) (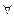 k ∈N) из истинности P(k) следует истинность Р(k + 1).
Тогда Р(n) истинно (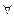 n ∈N).

Условие а) называют базисом индукции. Посылку Р(k) ― индуктивным предположением; утверждение б) ― индуктивным шагом.

Выделим основные шаги доказательства некоторого утверждения Р(n) методом математической индукции.

1. Формулировка утверждения Р(n), n ∈ N;

2. Формулировка и проверка истинности базиса индукции (Р(1) ― истинно);

3. Формулировка индуктивного предположения Р(k);

4. Формулировка и доказательство индуктивного шага
Р(k) → Р(k+ 1);

5. Вывод: (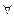 n ∈N) Р(n) ― истинно.

П р и м е р: доказать тождество:

.

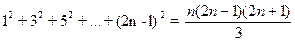Д о к а з а т е л ь с т в о:

Обозначим через S _n = 1² + 3² +... + (2n ― 1)².

Тогда утверждение

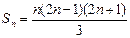
обозначим через Р(n).

Формулировка и проверка базиса индукции:

а) 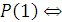«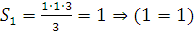», т.е. [P(1)]=1;

б) Индуктивное предположение:

[P(k)]=1 «».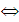

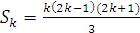Формулировка и доказательство индуктивного шага:

а) из истинности Р(k) следует истинность Р(k+1), т.е. нужно доказать, что из того, что

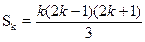
будет следовать, что

.

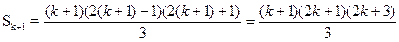б) Действительно,

,

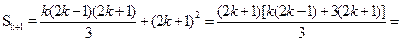
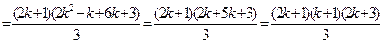т.е. Р(k+1) ― истинно.

Вывод: согласно принципа математической индукции,
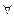n ∈N Р(n) ― истинно.