Предикаты и кванторы

Предикаты

Даже самые элементарные разделы математики (например, уравнения и неравенства) не могут быть полностью описаны лишь средствами исчисления высказываний. Это связано с тем, что в этой теории высказывание ― нерасчленяемый объект, не обладающий никакими свойствами, кроме как быть истинным или ложным. Дальнейшим развитием теории высказываний является теория предикатов. Логика предикатов начинается с анализа структуры элементарных высказываний. Высказывание расчленяется на терм и предикат. Терм ― это объект, о котором говорится в высказывании, а предикат ― это свойство, которым этот объект обладает или отношение, в котором он находится с другими объектами. Например: «2 ― четное число», «2» ― терм, «быть четным числом» ― предикат, или «3<5», «3», «5» ― термы, «меньше» ― предикат. Эти свойства и отношения определяют функцию, аргументы которой принимают значения из некоторого множества М, а областью значений является множество {0, 1}. В данном случае «х<у», «х ― четное число». Если вместо х и у подставлять любые числа из множества R, то будем получать либо истинные, либо ложные высказывания.
О п р е д е л е н и е: Функция F (х_1, х_2,..., х_n), определенная на множестве М и принимающая значения из множества {0, 1}, называется n- местным предикатом (n- местной высказывательной формой).

Таким образом, например, F(х) ― это одноместный предикат или одноместная высказывателъная форма, которая становится высказыванием, если вместо переменной х подставить любое значение из некоторого множества М. Так, например, если F(x) = х² + х ― 2 = 0 и М = R, то для х=2 F(2) =2² + 2– – 2 = 4 ≠ 0, [F(2)] = 0, т.е. получили ложное высказывание; если х = 1, то F(1) = 1²+1-2 = 0, [F(l)] = 1, то есть получили истинное высказывание.

Любое высказывание является нуль-местным предикатом и обоз­начается F⁰.

Итак, в логике предикатов рассматривают символы трех видов, связанные с множеством М и множеством {0, 1}:

а) предметные постоянные а, b, с,..., d ∈M;

б) предметные переменные х, у, z,..., принимающие значения из множества М;

в) переменные высказывания А, В, С, …,принимающие значения из множества {0,1}.

Если на множестве М задан n- местный предикат
F (х_1, х_2,...., х_n), то множество М разбивается на два множества: М=А 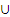В, на одном из множеств предикат принимает истинное значение, на другом ― ложное. Первое множество А называется множеством истинности предиката.

Например, множеством истинности любого уравнения или неравенства (например, F(х, у)=х²+у²­­-5=0) является множество его решений.

На множестве предикатов (высказывательных форм) можно определить отношение равносильности.

О п р е д е л е н и е: Два предиката F(х_1, х_2,...., х_n) и
P(х_1, х_2,...., х_n) от од­них и тех же переменных называются равносильными, если они имеют одно и то же множество истинности. Обозначение: F (х_1, х_2,...., х_n)⇔P (х_1, х_2,...., х_n).

Например, (х + 5 = 7) ⇔(х = 2), (х² + 1 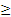0) ⇔(х ∈ R).

Отношение равносильности на множестве предикатов является отношением эквивалентности, так как оно определяется через отношение равенства множеств их истинности, а отношение равенства есть отношение эквивалентности на любом множестве.

С помощью логических операций (&, ∨,...) из данных высказывательных форм можно строить более сложные высказывательные формы.

Например, Р(х, у) & Q (х_: у) → В (х, у) ∨ С (х).

Из определения предиката (высказывательной формы), ясно, как получить высказывание ― для этого нужно вместо переменных подставить некоторые значения из множества М. Например, подставив вместо х, у, z действительные числа 3, 4, 5 в предикат х²+y²=z², получим «9+16=25» ― истинное высказывание. Если подставить числа 1, 0, 2, то получим «1=4» ― ложное высказывание.

Однако из предикатов можно получать высказывания и другим путем. Для этого вводятся так называемые операции «навешивания кванторов».

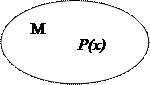Пусть одноместный предикат Р(х) задан на множестве М, тогда под символами ( 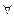х ∈М) Р(х) и ( 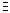х ∈М) Р(х) понимаем высказывание: «Для любого х ∈M Р(х)» и «существует х ∈М такое, что Р(х)».

Слова «для любого х» кратко обозначают символом 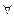х и называют квантором общности по переменной х. Слова «существует такой х, что...» обозначают символом 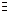х и называют квантором существования.

Высказывание 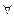х ∈М Р (х) считается истинным, если все элементы множества М обладают свойством Р и будет ложным, если найдется хотя бы один элемент, который этим свойством не обладает.

Например, [(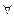 х ∈ R)(| х |>0)]=0, так как для х=0, | х |=0. Иными словами, квантор общности обобщает логическую операцию «конъюнкция» на бесконечном множестве.

Например, если М = {4, 8, 10}, Р (х) ― «х делится на 2», то (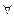 х ∈М) Р(х) ⇔ Р( 4 ) & Р( 8 ) & Р( 10 ).

Высказывание (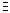 х ∈М) Р(х) считается истинным, если хотя бы один элемент множества М обладает свойством Р и будет ложным, если ни один элемент множества М этим свойством не обладает.

Квантор существования обобщает логическую операцию «дизъюнкция» на бесконечном множестве.

Если М={ а₁, а₂,..., а_n,... }, то

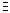( х ∈М) Р(х) ⇔ Р(а₁) ∨ Р(а₂) ∨ ... ∨ P(a_n) ∨ ...

Важно подчеркнуть, что истинность (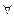 х ∈М) Р(х) и
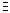( х∈М) Р(х) часто зависит от области определения предиката М. Например, [ ( 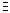х ∈Q )(x² = 2) ]=0, a [ ( 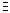х ∈ R) (x² = 2) ]=1.

Пусть теперь дана высказывательная форма (предикат), например, от трех переменных: F(х, у, z) ⇔ (х+y=z). Тогда
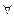( х ∈ 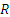)( 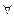y ∈ R)( 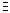х ∈М)(х+у=z) будет истинным высказыванием (для любой пары действительных чисел существует их сумма). А что будет собой представлять такая запись:

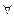( х ∈ R)( 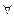y ∈ R) (х+у=z)?

Это предложение не зависит от переменных х и у, а зависит только от z, то есть является одноместным предикатом F(z).

Если на n- местный предикат F(х_1, х_2,...., х_n) навесить квантор 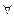х или 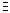х, то местность предиката уменьшится на 1. Например: ( 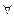x ∈ R)(x+y-z= 0) ― двухместный предикат;
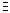( x ∈ R)( 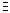y ∈ R)(х+у-z =0) ― одноместный предикат.

Для того, чтобы, из n- местного предиката получить высказывание, необходимо на все переменные навесить кванторы, или иначе говорят «связать их кванторами».

Вопросы для самоконтроля

1. Что называется высказывательной формой (предикатом)?

2. Какие высказывательные формы называют равносильными?

3. Каким образом из предикатов можно получить высказывания?

4. В чем состоит различие между «свободными» и «связанными» переменными?

5. Одноименные кванторы можно навешивать в любом порядке. Разноименные кванторы переставлять местами нельзя. Почему? Как это объяснить?