2015-02-27
362
1. Из таблицы в соответствии с номером варианта N (номер по списку группы) выбрать выражение исходной ФАЛ:
| N | Выражение | N | Выражение |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
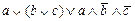
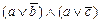
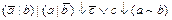
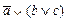
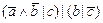
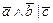
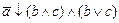
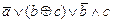
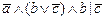
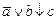
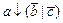
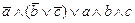
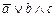
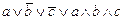
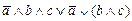
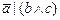
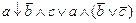
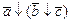
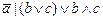
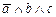
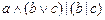
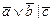
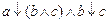
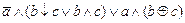
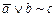
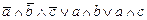
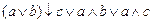
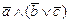
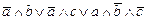
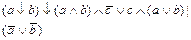
2. Определить тип и количество логических элементов, необходимых для реализации исходной ФАЛ:
| Тип | Реализуемая операция | Количество ЛЭ |
…………………………………………………………
| Всего |
Например, реализация ФАЛ у =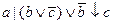 
требует логические элементы:
| Тип | Реализуемая операция | Количество ЛЭ |
| НЕ | Инверсия | |
| ИЛИ | Дизъюнкция | |
| И-НЕ | Штрих Шеффера | |
| ИЛИ-НЕ | Стрелка Пирса | |
| Всего |
3. Упростить исходное выражение до двух логических операций.
Чтобы получить компактную запись сложного выражения, прежде всего, целесообразно заменить в нем такие элементарные ФАЛ, как стрелка Пирса, штрих Шеффера, исключающее ИЛИ и эквивалентность их сложной формой записи. При этом необходимо помнить, что порядок вычисления логического выражения определяется тремя основными факторами:
|
|
|
– скобки. Выражения в скобках всегда вычисляются первыми;
– приоритет операций. По убыванию приоритета логические операции располагаются в следующем порядке:
§ инверсия отдельного аргумента,
§ штрих Шеффера, стрелка Пирса, эквивалентность,
§ конъюнкция,
§ операции типа дизъюнкции – собственно дизъюнкция и исключающее ИЛИ (неравнозначность);
– когда порядок вычисления выражения не задан скобками, а уровень приоритета операций одинаков, выражение вычисляется слева направо.
Например, выражение 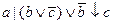следует переписать как 
.
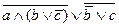Затем в полученном выражении с помощью законов и тождеств алгебры логики, а также сложной формой записи элементарных ФАЛ добиваются наименьшего числа операций. При этом в случае использования закона двойственности знак общей инверсии преобразуется в скобки.
Так, для приведенного примера:
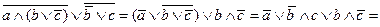
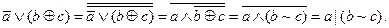
4. С помощью системы MATLAB проверить эквивалентность исходной и упрощенной ФАЛ.
Различные ФАЛ от одного и того же количества аргументов эквивалентны, если на всем множестве входных двоичных наборов их значения совпадают.
В системе MATLAB значения ФАЛ можно получить следующим образом. В командном окне (Command Window) системы MATLAB построчно в виде векторов-строк вводятся значения аргументов ФАЛ в соответствии с последовательностью входных двоичных наборов (табл. 1). При этом соседние элементы вектора-строки разделяются пробелом, а командная строка завершается символом «;», который означает запрет вывода на экран результата выполнения данной командной строки после перехода на следующую строку путем нажатия клавиши Enter.
|
|
|
После этого в очередной командной строке вводится ФАЛ, логическое выражение которой записывается с помощью стандартных для языка MATLAB операторов или функций (табл. 2). При этом в конце командной строки символ «;» не ставится, что после нажатия клавиши Enter обусловливает вывод на экран результатов вычислений в виде вектора-строки с указанием имени функции (см. табл. 1).
Пример записи ФАЛ с помощью операторов языка MATLAB приведен в табл. 1. Конечно, ФАЛ можно записать и с помощью только функций MATLAB, например
Y1=or(not(and(A,or(B,not(C)))),not(or(not(B),C))),
Y2=not(and(A,not(xor(B,C)))).
Но тогда выражения становятся громоздкими, что повышает вероятность ошибки как при записи, так и вводе в рабочее поле того или иного окна MATLAB.
5. Определить тип и количество логических элементов, необходимых для реализации полученной ФАЛ. На основании сравнения с таблицей п.2 работы сделать вывод относительно целесообразности упрощения ФАЛ.
