С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость все состояния равновесия системы
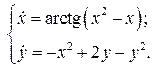
Решение. Для нахождения состояний равновесия решим систему уравнений
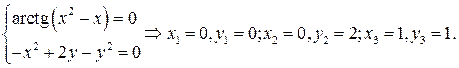
Итак, рассматриваемая система имеет следующие состояния равновесия: 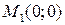 ,
, 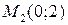 и
и 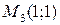 .
.
Найдем матрицу Якоби системы: 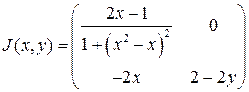 .
.
Для точки 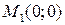 матрица Якоби имеет вид
матрица Якоби имеет вид 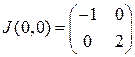 . Ее собственные значения
. Ее собственные значения 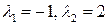 . Поэтому решение
. Поэтому решение 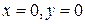 неустойчиво по Ляпунову.
неустойчиво по Ляпунову.
С помощью пакета Maple построим фазовый портрет рассматриваемой системы в окрестности начала координат.
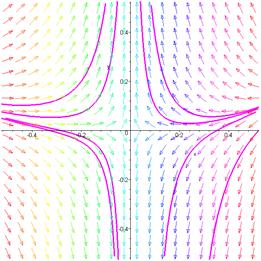

Рис. 5.1. Фазовый портрет системы в окрестности точки 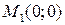
Для точки 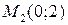 матрица Якоби имеет вид
матрица Якоби имеет вид 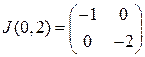 . Ее собственные значения
. Ее собственные значения 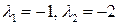 . Поэтому решение
. Поэтому решение 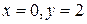 асимптотически устойчиво по Ляпунову.
асимптотически устойчиво по Ляпунову.
С помощью пакета Maple построим фазовый портрет рассматриваемой системы в окрестности точки 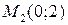 .
.
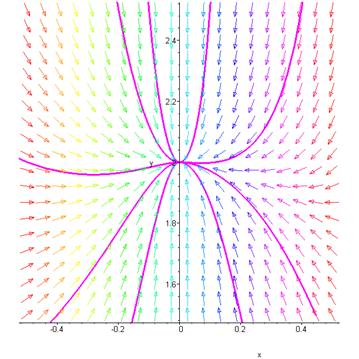
Рис. 5.2. Фазовый портрет системы в окрестности точки 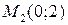
Для точки 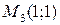 матрица Якоби имеет вид
матрица Якоби имеет вид 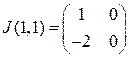 . Ее собственные значения
. Ее собственные значения 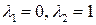 . Поэтому решение
. Поэтому решение 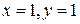 неустойчиво по Ляпунову.
неустойчиво по Ляпунову.
С помощью пакета Maple построим фазовый портрет рассматриваемой системы в окрестности точки 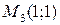 .
.
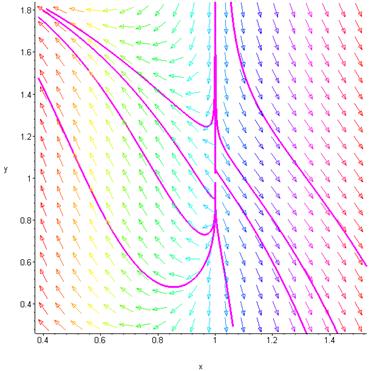
Рис. 5.3. Фазовый портрет системы в окрестности точки 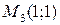
 2015-02-27
2015-02-27 604
604








