С помощью теоремы об устойчивости по первому приближению найти значения параметров a и b, при которых асимптотически устойчиво нулевое решение системы
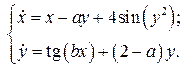
Решение. Система первого приближения в данном случае имеет вид:
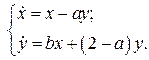
Составим соответствующее ей характеристическое уравнение:
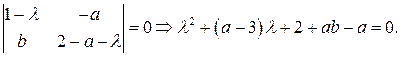
Оба корня полученного уравнения будут иметь отрицательные вещественные части, если выполняются условия 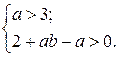 . Область асимптотической устойчивости рассматриваемой системы на плоскости
. Область асимптотической устойчивости рассматриваемой системы на плоскости 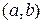 изображена на расположенном ниже рисунке.
изображена на расположенном ниже рисунке.


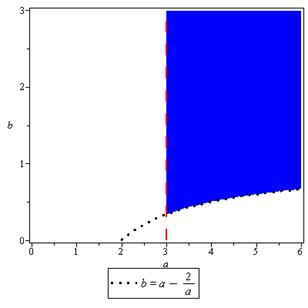

Рис. 5.4. Область асимптотической устойчивости в пространстве параметров
Результаты численного интегрирования рассматриваемой системы показывают, что при 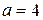 ,
, 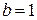 точка покоя
точка покоя 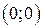 является устойчивой (устойчивый фокус), а при
является устойчивой (устойчивый фокус), а при 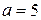 ,
, 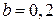 - неустойчивой (точка покоя типа «седло»).
- неустойчивой (точка покоя типа «седло»).
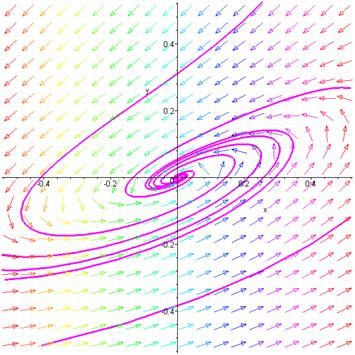
Рис. 5.5. Фазовый портрет системы при 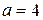 ,
, 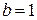
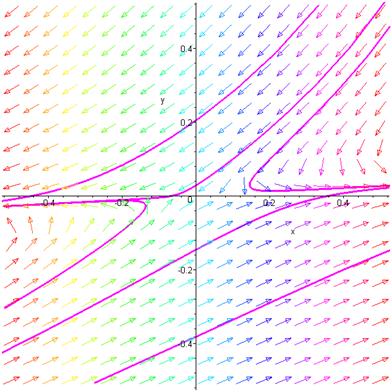
Рис. 5.6. Фазовый портрет системы при 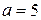 ,
, 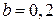
 2015-02-27
2015-02-27 401
401








