2015-02-27
507
Задание. Локализовать наименьший положительный корень уравнения и уточнить его значение заданным методом с точностью до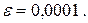 
| № варианта | Уравнение | № варианта | Уравнение |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
 
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
| 
| ||
| 
| ||
| 
| ||
| 
|
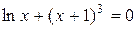
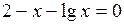
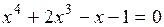
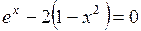
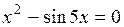
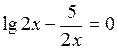
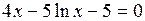
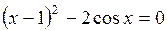
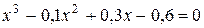
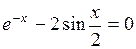
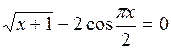
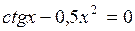
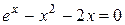
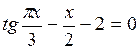
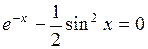
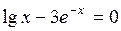
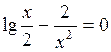
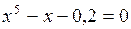
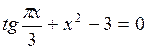
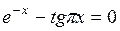
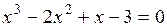
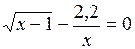
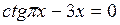
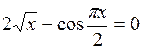
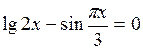
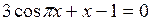
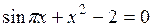
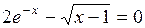
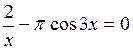
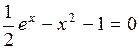
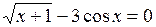
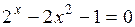
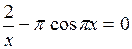
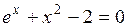
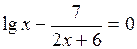
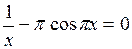
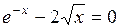
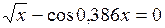
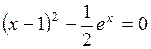
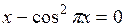
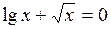
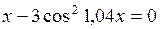
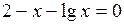
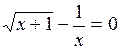
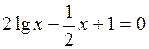
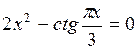
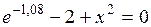
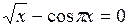
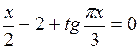
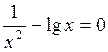
Лабораторная работа №3. «Решение систем линейных алгебраических уравнений»
Цель работы:
- Изучение следующих учебных элементов:
· точные методы решения систем линейных алгебраических уравнений (метод Гаусса, метод Крамера, матричный метод);
· приближенные методы решения систем линейных алгебраических уравнений (простых итераций, Зейделя);
· условия сходимости и окончания вычислительного процесса при использовании приближенных методов;
· сравнительная характеристика методов решения систем линейных уравнений.
- Численное решение конкретной системы линейных алгебраических уравнений.
Задание. Методом простой итерации или методом Зейделя решить систему линейных уравнений с точностью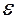 
=10-3.
| № | Система | № | Система |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
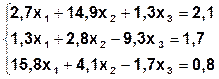
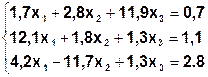
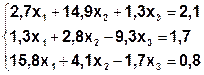
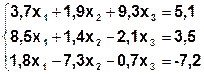
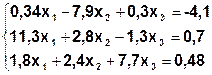
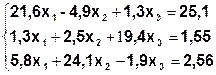
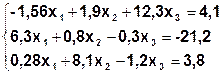
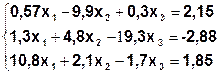
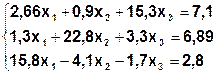
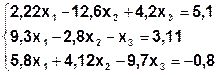
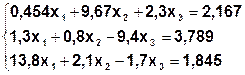
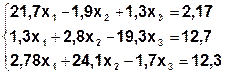
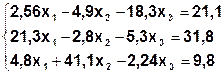
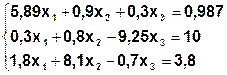
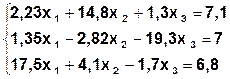
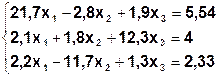
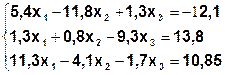
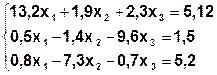
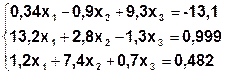
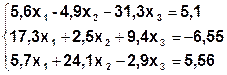
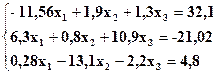
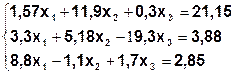
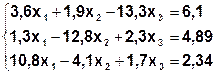
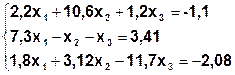
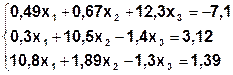
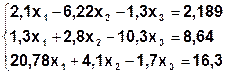
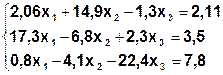
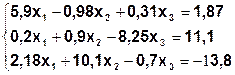
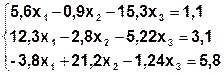
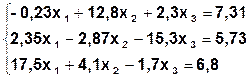
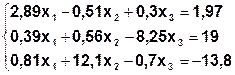
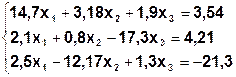
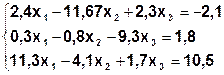
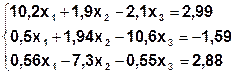
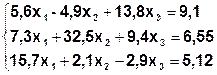
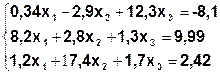
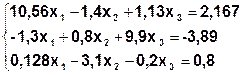
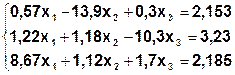
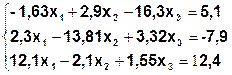
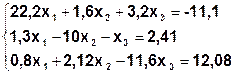
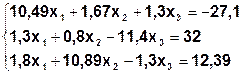
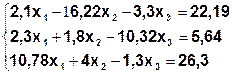
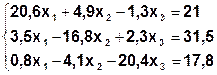
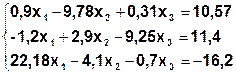
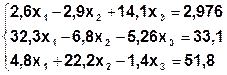
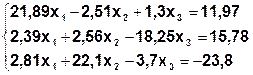
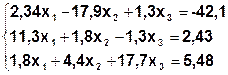
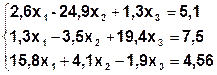
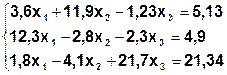
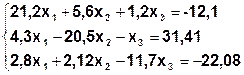
Лабораторная работа №4. «Численное интегрирование»
Цель работы:
- Изучение следующих учебных элементов:
· общая идея методов численного интегрирования;
· методы прямоугольников, трапеций, Симпсона;
· правило Рунге;
· сравнительная оценка методов численного интегрирования.
- Приближенное вычисление конкретного определённого интеграла.
Задание. Найти определенный интеграл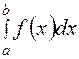 
с точностью 
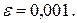Метод вычисления определяется преподавателем.
| № | а | b | f(x) | № | а | b | f(x) |
| 0,6 | 1,5 |
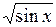
| 1,2 |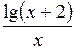 
| |||
| 1,2 | 2,832 |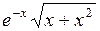 
| 1,6 | 2,4 |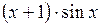 
| ||
| 1,3 | 2,956 |
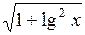
| 0,2 |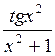 
| |||
| 2,8 | 4,408 |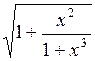 
| 0,6 | 1,4 |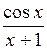 
| ||
| 0,8 | 2,528 |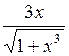 
| 0,4 | 1,2 |
| ||
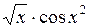
| -0,52 | 1,58 |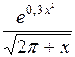 
| 0,8 | 1,2 |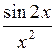 
| ||
| 0,2 | 2,12 |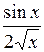 
| 0,8 | 1,6 |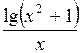 
| ||
| 1,5 | 3,42 |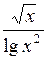 
| 0,4 | 1,2 |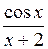 
| ||
| 1,1 | 2,876 |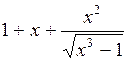 
| 0,4 | 1,2 |
| ||
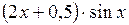
| 0,31 | 1,93 |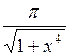 
| 0,4 |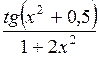 
| |||
| 1,5 | 3,18 |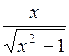 
| 0,18 | 0,98 |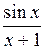 
| ||
| -1,3 | 0,476 |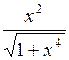 
| 1,4 |
| |||
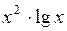
| 1,0 | 2,76 |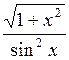 
| 1,4 | 2,2 |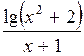 
| ||
| 2,4 | 4,08 |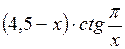 
| 0,4 | 1,2 |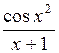 
| ||
| 1,82 | 3,464 |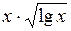 
| 0,8 | 1,6 |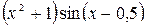 
| ||
| 1,5 | 3,24 |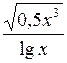 
| 0,6 | 1,4 |
| ||
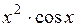
| 1,4 | 3,008 |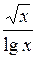 
| 1,2 |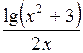 
| |||
| -0,2 | 1,252 |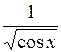 
| 2,5 | 3,3 |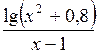 
| ||
| 0,15 | 1,878 |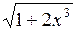 
| 0,5 | 1,2 |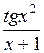 
| ||
| -0,52 | 1,58 |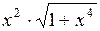 
| 1,3 | 2,1 |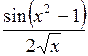 
| ||
| 0,3 | 1,844 |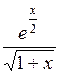 
| 0,2 | 1,0 |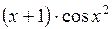 
| ||
| 3,5 | 4,94 |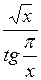 
| 0,8 | 1,2 |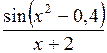 
| ||
| 1,44 |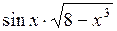 
| 1,2 | 2,8 |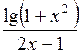 
| |||
| 5,1 | 6,54 |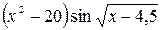 
| 0,6 | 0,72 |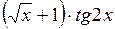 
| ||
| 1,42 | 2,98 |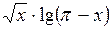 
| 0,8 | 1,2 |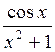 
|
Лабораторная работа №5. «Аппроксимация функций с помощью метода наименьших квадратов»
Цель работы:
- Изучение следующих учебных элементов:
· постановка задачи математической обработки данных;
· сущность метода наименьших квадратов;
· геометрическая интерпретация метода наименьших квадратов;
· нахождение параметров линейной, квадратичной, степенной и показательной приближающих функций.
