Метод трапеций

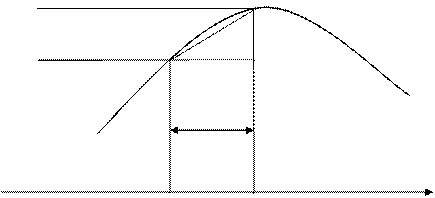
В соответствии с полученными ранее формулами «левых» и «правых» прямоугольников истинное значение интеграла лежит между приближенными значениями, определяемыми по этим формулам (рис. I. 2), т.е. лучшую формулу численного интегрирования можно получить, взяв среднее арифметическое этих значений:

Рис. 1. 2

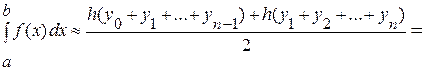
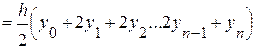
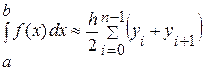. (I. 4)

Эта формула (I. 4) описывает метод трапеций для численного интегрирования, т.е. приближенное значение интеграла 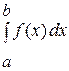получается в виде суммы площадей «n» трапеций.