2015-02-04
264
(Методические указания и задания)
Составители С.И. Смуров
В.А. Таланова
С.П. Бобков
Иваново 2003
В методических указаниях рассматриваются методы приближенного вычисления определенного интеграла, численного решения алгебраических и трансцендентных уравнений, вопросы математической обработки экспериментальных данных.
Даны примеры решения задач и задания для самостоятельной работы.
Указания составлены в соответствии с программой и одобрены решением цикловой методической комиссией по физико-математическим дисциплинам.
1. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Вычислить определенный интеграл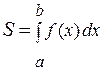 
, где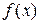 
– непрерывная функция x в интервале 
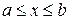, можно с помощью аналитической формулы, если использовать прием формального интегрирования по формуле Ньютона-Лейбница (I. I.)
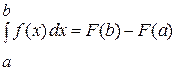, (I. I.)
где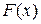 
– первообразная функция для заданной функции .
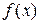Однако во многих случаях не удается найти никакой аналитической формулы в виду невозможности определения .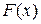
В таких случаях приходится применять методы численного интегрирования.
Основной принцип построения всех приближенных формул численного интегрирования состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая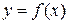 
заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить, используя ординаты на концах отрезков.
