Уточнение корней методом половинного деления

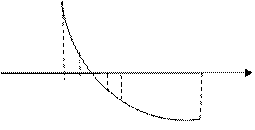
Пусть корень уравнения 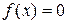отделен на отрезке [a, b], т.е. f(a)f(b)<0 и f ’ (x) сохраняет знак (рис. 2.6.).

Рис. 2.6

В качестве начального приближения корня возьмем точку c₀ – середину отрезка: 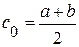. Если f(с₀)=0, то c₀ – искомый корень уравнения, если 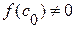, то из двух отрезков [a, c₀] и [c₀, b] выбираем тот, на концах которого функция принимает значение разных знаков.

Новый отрезок опять делим пополам и далее поступаем аналогично вышеизложенному. Длина каждого нового отрезка вдвое меньше длины предыдущего отрезка, т.е. за n шагов сократится в 2ⁿ раз.

Вычисления прекращаем, если длина отрезка 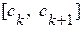станет меньше заданной погрешности 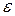, т.е. .

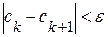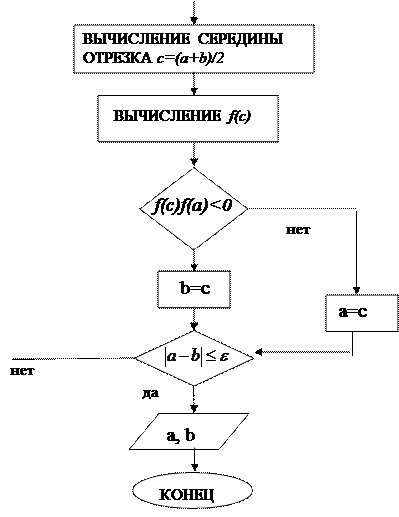
Блок-схема метода половинного деления